SOLUTION: Help on this please A freight train is carrying goods across the country. The distance it has traveled varies directly with the number of gallons of fuel it has used. See the gr

Algebra ->  Graphs -> SOLUTION: Help on this please A freight train is carrying goods across the country. The distance it has traveled varies directly with the number of gallons of fuel it has used. See the gr      Log On


   

Question 1182672: Help on this please
A freight train is carrying goods across the country. The distance it has traveled varies directly with the number of gallons of fuel it has used. See the graph below.

https://imgur.com/a/igCQtj2
How many miles does the train travel per gallon?
What is the slope of the graph?
Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!
train

from the graph you can see points is (100,50), (200,100), and (400,200)
which means that train uses 100+gallons to travel 50 miles
which means that train uses 200+gallons to travel+100 miles
which means that train uses 400 gallons to travel 200+miles
the ratio is:
50mil%2F100gal=100mil%2F200gal=200mil%2F400gal+=%281%2F2%29%28mil%2Fgal%29
so, answer is: the train travel 1%2F2 miles per gallon

What is the slope of the graph?
use two points above
(100,50), (200,100)
m=%28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29
m=%28100-50%29%2F%28200-100%29
m=50%2F100
m=1%2F2
equation of this line is
y-y%5B1%5D=m%28x-x%5B1%5D%29
y-50=%281%2F2%29%28x-100%29
y-50=%281%2F2%29x-%281%2F2%29100
y-50=%281%2F2%29x-50
y=%281%2F2%29x-50%2B50
y=%281%2F2%29x








Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

Help on this please
A freight train is carrying goods across the country. The distance it has traveled varies directly with the number of gallons of fuel it has used. See the graph below.

https://imgur.com/a/igCQtj2
How many miles does the train travel per gallon?
What is the slope of the graph?
1. From the graph, one of the intersection points is: (50, 100), which means that to cover 50 miles, takes 100 gallons, or . 

   In other words, in travelling 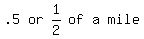matrix%281%2C6%2C+.5%2C+or%2C+1%2F2%2C+of%2C+a%2C+mile%29, 1 gallon of fuel is used.

2. From the graph, start at point (0, 0), or the origin. Move UP the y-axis to 50, and then RIGHT, to x = 100, or intersection point: (50, 100).

   This gives you