Question 118193: is there more than one way to solve inequalities, perhaps a shortcut?
can you show me using an example?
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solving linear inequalities is  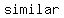 to solving to solving 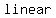 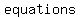 , except for one detail: you , except for one detail: you 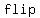 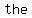 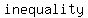  whenever you multiply or divide the inequality by a whenever you multiply or divide the inequality by a 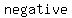 . .
Use the addition, subtraction, multiplication, and division properties of inequalities to solve linear inequalities. We always want to get the variable on one side and everything else on the other side by using inverse operations.
some examples:
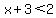 add
add  to the both sides to the both sides
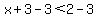

Solution are all  values from values from  to to  , where , where  is excluded. is excluded.
We can write it like this: interval ( , , ) )
As you can see from this example, the only difference here is that you have a "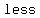 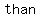 " sign, instead of an " " sign, instead of an "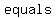 " sign. " sign.
Note that the solution to a "less than, but not equal to" inequality is graphed  a a 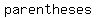 (or else an open dot) at the endpoint. (or else an open dot) at the endpoint.
 ..move
..move  to the left and to the left and  to the right to the right
 ..
..
 ..
..
Solution are all  values from values from  to to  , where , where  is included. is included.
We can write it like this: interval ( , , ] ]
Note that the solution to a "less than or equal to" inequality is graphed with a bracket (or else a closed dot) at the endpoint.

 ......divide both sides by ......divide both sides by  (remember, you flip the sign ) (remember, you flip the sign )



Graphing Inequalities
When  is less than a constant (for example is less than a constant (for example 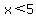 ), you darken in the part of the number line that is ), you darken in the part of the number line that is 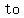 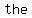  of the of the 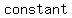 . .
Also, because there is  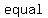 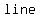 , we are , we are  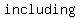 where where  is equal to the constant. is equal to the constant.
That means we are not including the 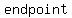 . One way to notate that is to use an open hole at that point. . One way to notate that is to use an open hole at that point.
When  is greater than a constant (for example is greater than a constant (for example 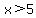 ), you darken in the part of the number line that is to the right of the constant. ), you darken in the part of the number line that is to the right of the constant.
Also, because there is  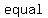 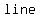 , we are , we are  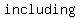 where where  is equal to the constant. is equal to the constant.
That means we are not including the endpoint. One way to notate that is to use an open hole at that point.
When  is less than or equal to a constant (for example is less than or equal to a constant (for example  ), you darken in the part of the number line that is to the left of the constant. ), you darken in the part of the number line that is to the left of the constant.
Also, because there is an equal line, we are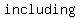 where where  is equal to the constant. That means we are is equal to the constant. That means we are 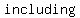 the endpoint. One way to notate that is to use an closed hole at that point. the endpoint. One way to notate that is to use an closed hole at that point.
When  is greater than or equal to a constant (for example is greater than or equal to a constant (for example  ), you darken in the part of the number line that is to the right of the constant. ), you darken in the part of the number line that is to the right of the constant.
Also, because there is an equal line, we are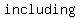 where where  is equal to the constant. That means we are is equal to the constant. That means we are  the endpoint. One way to notate that is to use an closed hole at that point. the endpoint. One way to notate that is to use an closed hole at that point.
Properties for Inequalities:
Addition/Subtraction Property for Inequalities
If 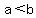 , then , then 
If 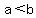 , then , then 
Multiplication/Division Properties for Inequalities
when multiplying/dividing by a positive value
If 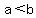 AND AND 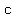 is positive, then is positive, then 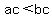
If 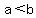 AND AND 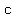 is positive, then is positive, then 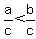
|
|
|