SOLUTION: This is more polynomials but I could not find a section for that. im sorry if there is.its my first time on here. for what real values of k does the equation x^3 - 2x^2 - 4x +

If you rewrite the equation in this EQUIVALENT form,

    x^3 - 2x^2 - 4x = -k,


then you can re-formulate the question in this EQUIVALENT form


    +-------------------------------------------------------------- ------+
    |              for what real values of k the equation                 |
    |    x^3 - 2x^2 - 4x = -k  has at least one root between -2 and 0 ?   |
    +---------------------------------------------------------------------+


Now look into this plot of the polynomial  p(x) = x^3 - 2x^2 - 4x.



    


                   Plot y = x^3 - 2x^2 - 4x 



From this Figure, identify that part of the plot, which is over the interval (-2,0).


Over this interval, the plot makes a downward cup.


The values of "-k"  (note: "minus k")  we are seeking for, are the values on y-axis  of the polynomial p(x) over the interval (-2,0).



    So, now it is clear how to solve the problem:  the values of "-k" are from the negative value of 

        p(-2) =  = -8

    to 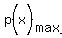   over the interval (-2,0).


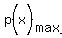Thus our task now is to find    over the interval (-2,0).


It is easy: it is a standard typical Calculus problem.

We must take the derivative of p(x); equate it to zero; find the optimum value of x and calculate p(x) at this value of x.


So, the derivative of p(x) is  p'(x) = 3x^2 - 4x - 4;  the root  of p'(x) = 0 is the root of the equation

    3x^2 - 4x - 4 = 0,

and over the interval (-2,0) it is  x =  =  =  =  =  = .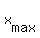


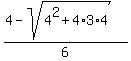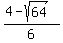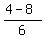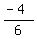Finally, 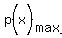  = 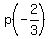 =  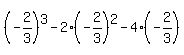= 1.481 (rounded).


Thus we found out that the values {-k} belong to the interval (-8,1.481).


It means that the values of "k" we are seeking for are in the interval  (-1.481,8).    ANSWER