Question 1178983: Solve the following inequality
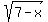 > > 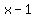
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve the following inequality 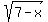 > x-1 > x-1
~~~~~~~~~~~~~~~
This inequality is SPECIAL and its solution requires ACCURACY - so trace attentively each my step.
1. The domain of this inequality is the set 7-x >= 0, or x <= 7.
2. All the set x-1 < 0, or x < 1, is the solution, BECAUSE the right side is negative there,
while the left side is not negative.
Therefore, we need analyze for the solution only the remaining part 1 <= x <= 7.
Let's call this set { 1 <= x <= 7 } as A17.
3. Next, analyzing for the set A17, square both sides of the original inequality. You will get
7 - x > x^2 - 2x + 1
x^2 - x - 6 < 0
(x-3)*(x+2) < 0
The solution set to the last inequality is -2 < x < 3.
Taking the intersection with the set A17, we have the solution set { 1 <= x <3 }.
4. Thus we have two parts of the entire solution set (a) { x < 1 } from n.2, and (b) { 1 <= x < 3 } from n.3.
The final solution set is the union sets (a) and (b), i.e. { x < 1 } U { 1 <= x < 3}, which is, OBVIOUSLY, (-oo < x < 3 }.
ANSWER. The solution to the original inequality is the set { -oo < x < 3 }, or (-oo,3).
Visual CHECK
 Plot y =
Plot y = 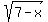 (red line) and y = x-1 (green line)
The solution set is the set of all points of the x-axis, where red line is above the green line. (red line) and y = x-1 (green line)
The solution set is the set of all points of the x-axis, where red line is above the green line.
Solved, answered, explained, visualized, checked and completed.
////////////
The post-solution note
The plot is indispensable helper in such an analysis.
Honestly, it is THE PLOT, who directs and guides the flow of your mental reasonings.
///////////
Do not forget to post your "THANKS" to me for my teaching.
|
|
|