Question 1178347: 7. The path of a baseball after it is hit is modelled by the equation h=-4.98t^2+12.51t+1.36, where h is the height, in metres, of the ball and t is the time, in seconds, after the ball is hit.
a. Find the maximum height that the ball reaches, to the nearest hundredth of a metre.
b. Determine the height of the ball, to the nearest hundredth of a metre, at 2.5 seconds.
c. Determine when the ball is at a height of 8m, to the nearest hundredth of a second. (2 marks)
d. State the y-intercept of the graph to the nearest hundredth. Describe what the y-intercept represents in the context of this question.
e.i. Find the coordinates of both x-intercepts of the graph to the nearest hundredth.
ii. State what the positive x-intercept represents in the context of this problem.
iii. Explain why the negative x-intercept is not valid in the context of this problem.
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
7. The path of a baseball after it is hit is modelled by the equation
 , where , where  is the height, in metres, of the ball and is the height, in metres, of the ball and is the time, in seconds, after the ball is hit. is the time, in seconds, after the ball is hit.
a. Find the maximum height that the ball reaches, to the nearest hundredth of a metre.
You have to take the derivative of the function and set it equal to . That's where the ball would reach it's top point. So the derivative is . That's where the ball would reach it's top point. So the derivative is
 .........solve this equation for .........solve this equation for 



Substitute this value of t into the original equation to get the maximum height.


b. Determine the height of the ball, to the nearest hundredth of a metre, at  seconds. seconds.

 m m
c. Determine when the ball is at a height of  , to the nearest hundredth of a second. (2 marks) , to the nearest hundredth of a second. (2 marks)


 .........using the quadratic formula we get .........using the quadratic formula we get
 seconds or seconds or seconds seconds
d. State the y-intercept of the graph to the nearest hundredth. Describe what the y-intercept represents in the context of this question.
The y-intercept occurs when  . So substitute . So substitute  into the equation. You get into the equation. You get  . What that means is that the ball STARTS at a height of . What that means is that the ball STARTS at a height of  meters, which would be the height of the bat when it hits the ball. meters, which would be the height of the bat when it hits the ball.
y-intercept is at ( , ,  ) )
e.i. Find the coordinates of both x-intercepts of the graph to the nearest hundredth.
set 
 .........using the quadratic formula we get .........using the quadratic formula we get
 or or

x-intercept is at (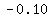 , ,  ) and ( ) and ( , ,  ) )
ii. State what the positive x-intercept represents in the context of this problem.
Time the ball hits the ground  seconds after being hit. seconds after being hit.
iii. Explain why the negative x-intercept is not valid in the context of this problem.
The ball is starting from a height of  m at m at  . Where it was before being hit is non-sequitur. . Where it was before being hit is non-sequitur.
|
|
|