Question 1178346: Each year, a baseball team sells boxes of chocolates as a fundraiser to lower the cost of team fees. The price of the chocolates and the number of boxes sold varies each year. The information from five years of sales is given in the table below.
Price per box ($)= 3.00/4.00/5.50/6.50/8.00
Boxes sold= 5303/3360/1777/1316/1019
a. Find the regression equation in the form y=ax^3+bx^2+cx+d that best approximates the data. Express the values of a, b, c, and d to the nearest hundredth.
b. Use the equation to find the number of boxes, to the nearest whole number, that the team will sell if they charge $4.35 per box.
c. One year, the team only sold 125 boxes of chocolates. What price did they charge for each box?
d. If the team raises the price too high, they will not sell any boxes. Use your regression equation to predict the price of a box that will result in zero boxes sold.
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a. Find the regression equation in the form
 ........Price per box ($)= ........Price per box ($)= 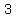 and Boxes sold= and Boxes sold= 

 ...........solve for ...........solve for 

 ...........eq.1 ...........eq.1
 ........Price per box ($)= ........Price per box ($)= 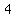 and Boxes sold= and Boxes sold= 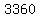

 ...........solve for ...........solve for 

 ...........eq.2 ...........eq.2
 ........Price per box ($)= ........Price per box ($)= 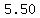 and Boxes sold= and Boxes sold= 

 ...........solve for ...........solve for 


 ...........eq.3 ...........eq.3
 ........Price per box ($)= ........Price per box ($)= 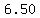 and Boxes sold= and Boxes sold= 
 ........solve for ........solve for 


 ........eq.4 ........eq.4
from eq.1 and eq.2
 ..........solve for ..........solve for 





 ....................eq.5 ....................eq.5
go to
 ...........eq.1, substitute ...........eq.1, substitute 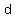

 ........................1) ........................1)
go to
 ...........eq.3, substitute ...........eq.3, substitute 

 ............2) ............2)
from eq.1) and 2)
 ........solve for ........solve for 
 ...............3) ...............3)
 ........................1) substitute ........................1) substitute 

 ...................................4) ...................................4)
go to
 ....................eq.5,substitute ....................eq.5,substitute 

 ........................5) ........................5)
go to
 ........eq.4, substitute ........eq.4, substitute  , , , and , and 






go to
 ...............3), substitute ...............3), substitute 


go to
 ........................5), substitute ........................5), substitute 


go to
 ...........eq.1, substitute ...........eq.1, substitute  , ,  ,and ,and 

solutions:
 ≈ ≈ , ,  ≈ ≈ , ,  ≈ ≈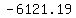 , ,  ≈ ≈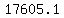
the regression equation is:

b. Use the equation to find the number of boxes, to the nearest whole number, that the team will sell if they charge $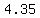 per box. per box.
 ....plug in ....plug in 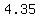 for for 


c. One year, the team only sold  boxes of chocolates. What price did they charge for each box? boxes of chocolates. What price did they charge for each box?
 ....plug in ....plug in  for for
 .....using calculator .....using calculator
->there is one real solution and it is  ≈ ≈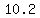
d. If the team raises the price too high, they will not sell any boxes. Use your regression equation to predict the price of a box that will result in zero boxes sold.
 .....using calculator .....using calculator
->there is one real solution and it is
 ≈ ≈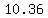
|
|
|