SOLUTION: The graph of f(x) is shown below. https://latex.artofproblemsolving.com/d/b/a/dba24dce7c2734af95b18f61b73b2a32f213cd79.png For each point (a,b) on the graph of y = f(x), the point

Algebra ->  Graphs -> SOLUTION: The graph of f(x) is shown below. https://latex.artofproblemsolving.com/d/b/a/dba24dce7c2734af95b18f61b73b2a32f213cd79.png For each point (a,b) on the graph of y = f(x), the point      Log On


   

Question 1165442: The graph of f(x) is shown below. https://latex.artofproblemsolving.com/d/b/a/dba24dce7c2734af95b18f61b73b2a32f213cd79.png
For each point (a,b) on the graph of y = f(x), the point ( 3a - 1, b/2) is plotted to form the graph of another function y = g(x). For example, (0,2) lies on the graph of y = f(x), so (3 * 0 - 1, 2/2) = (-1,1) lies on the graph of y = g(x).
(a) Plot the graph of y = g(x). Include the diagram in your solution.
(b) Express g(x) in terms of f(x).
(c) Describe the transformations that you would apply to the graph of y = f(x) to obtain the graph of y = g(x). For example, one transformation might be to stretch the graph horizontally by a factor of 5.
Please answer in detail!
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
This is the graph of f(x):



We translate the endpoints of the line segments in f(x) to line segments
in g(x), using the given point transformation (a,b) ---> (3a-1, b/2)

(-4,4) in f(x) corresponds to (-13,2) in g(x).
(-1,0) in f(x) corresponds to  (-4,0) in g(x).
 (0,2) in f(x) corresponds to  (-1,1) in g(x)
(4,-4) in f(x) corresponds to (11,-2) in g(x)



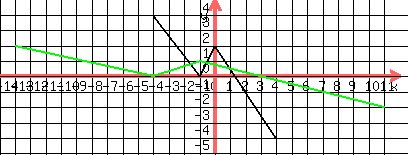f(x) is in black, g(x) is in green.

We observe what happens when point (a,b) on f(x) becomes (3a-1,b/2) on g(x)

Each x-coordinate "a" becomes "3a", and then becomes "3a-1"

When "a" becomes "3a", that indicated a horizontal stretch by a factor of 3.
That is accomplished by replacing x in f(x) by 1/3x,

So that gives us 

f%28expr%281%2F3%29x%29 

for "a" becoming "3a".

Then when "3a" becomes "3a-1", that indicates a horizontal shift by 1 unit
left. That is accomplished by replacing x by x+1.

So that gives us

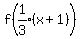f%28expr%281%2F3%29%28x%2B1%29%29 

for "3a" becoming "3a-1".

Now each y-coordinate "b" becomes "b/2".

When each y-coordinate "b" becomes "b/2", the graph is shrunk vertically
by a factor of 1/2.  That is accomplished by multiplying the entire function
by 1/2,

So that gives us

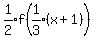expr%281%2F2%29f%28expr%281%2F3%29%28x%2B1%29%29

for b becoming b/2.

So that now completes g(x) in terms of f(x), so we have:

%22g%28x%29%22+=+expr%281%2F2%29f%28expr%281%2F3%29%28x%2B1%29%29

You will notice that the green graph is the black graph stretched
horizontally by a factor of 3, then shrunk vertically by a factor of 1/2 and
shifted left by 1 unit.

Edwin