SOLUTION: The line y=2x+c is a tangent to the curve y=2x^2-6x+20.find the value of c

f'(x) =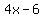 



For the tangent 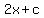 to just touch f(x), we need to find where f(x) has slope equal to 2:



    4x-6 = 2     <<< remember, the ENTIRE LHS is the slope of f(x)

     x = 2        





At x=2:  f(2) = 



So the tangent line 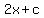 just meets f(x) at x=2, hence it has value 16 there:



     2x + c = 2(2) + c = 16  ==> c = 12





Ans:    and the tangent line is  y=2x+12, and the point of tangency is (2,16).