Question 1156565: The problem is stated thus: A circle is tangent to the y-axis at y=3 and has one x-intercept at x=1.
a. Determine the other x-intercept
b. deduce the equation of the circle
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
The problem is stated thus: A circle is tangent to the y-axis at y=3 and has one x-intercept at x=1.
a. Determine the other x-intercept
b. deduce the equation of the circle
~~~~~~~~~~~~~~
Let "r" be unknown radius of the circle.
Then its center is at the point (r,3), from the condition.
The distance from the circle's center to y-axis is "r".
The distance from the center to the point (1,0) is "r", again.
These distances are equal as the radii of the circle, which gives you this equation
r =  .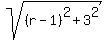
To solve the equation, square its both sides
r^2 = (r-1)^2 + 3^2).
r^2 = = r^2 - 2r + 1 + 9
2r = 10
r = 10/2 = 5.
So, the center of the circle is the point (5,3) and its radius is 5 units.
Therefore, the equation of the circle is
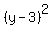 +  = 5^2. (1).
The other x-intersection point is (9,0). // It is so, because 9 = 5 +(5-1). Try to understand what does it mean and why it is RELEVANT.
--------------------
If you have questions regarding my solution, you may post them to me.
If you do, THEN refer to the problem ID number 1156565.
If you do not refer to the problem's ID number, I will not know to whom to respond --- and, therefore, will not respond, at all.
Happy learning (!)
It is a good problem and it assumes that you will turn on your brain and will make efforts to understand the solution in full.
Answer by MathLover1(20849)  (Show Source):
|
|
|
