Question 1147059: Hi, I have a question concerning me before a test. The problem is that Jake needs to buy 120 beverages. X is packs of 8 for juice and y is packs of 12 for water. We have to write it in standard form and so far I have tried 8x + 12y = 120 and that would mean that y = 10 and x = 15. I was just wondering if that is correct. Thanks
Found 4 solutions by josmiceli, MathTherapy, greenestamps, ikleyn:
Answer by josmiceli(19441)   (Show Source):
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! Hi, I have a question concerning me before a test. The problem is that Jake needs to buy 120 beverages. X is packs of 8 for juice and y is packs of 12 for water. We have to write it in standard form and so far I have tried 8x + 12y = 120 and that would mean that y = 10 and x = 15. I was just wondering if that is correct. Thanks
Your answers are NOT correct, but your equation is, but you need to be consistent, as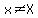 
I'll use the lower case variable. This will give: 
You should realize that the number of packs of juice, as well as the number of packs of water MUST have integer values.
If you look at the equation:  , it's obvious that y, or the number of packs of water, can be 10. If you substitute that value for y, you'll get an INTEGER value for the number of packs of juice.
Now, since we need to decrease the number of packs of water (increasing this number will lead to a NEGATIVE number of packs of juice), the next integer value, down from 10 is 9.
If 9 is used, you'll get a NON-INTEGER value for the packs of juice. So, 9 DOESN'T work. If you continue, you'll notice that ONLY EVEN VALUES of packs of water, from 10, down to 0, will work.
Therefore, your answer will be varying packs of juice, depending on the varying EVEN-NUMBER of packs of water, from 10, down to 0, or from 0 to 10.
If you're confused, this is what you should get: 
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
You don't make it clear what you are supposed to do. If indeed all you are asked to do is write an equation representing the given situation, then you are finished when you write
8x+12y = 120
If you need to find A solution, then you can do some trial and error. Or you can do what you did and find that two easily identified solutions are (x,y) = (15,0) and (x,y) = (0,10).
The most interesting problem would to be to find ALL the solutions. In the context of the problem, that means finding all the solutions in non-negative integers.
A standard way to do that is to solve the equation for one variable in terms of the other and use the requirement that the solutions have to be integers to find the solutions.
You can solve for either variable; in this problem I think it will be easier to solve for y.
Given this form of the equation, and knowing y has to be an integer, we can conclude that (2/3)x must be an integer; and that means x must be a multiple of 3. Then remembering that both x and y must be non-negative, we can find all the solutions:
x y=10-(2/3)x (x,y)
-------------------------
0 10 (0,10)
3 10-2 = 8 (3,8)
6 10-4 = 6 (6,6)
9 10-6 = 4 (9,4)
12 10-8 = 2 (12,2)
15 10-10 = 0 (15,0)
Answer by ikleyn(52780)  (Show Source):
|
|
|
