Question 1141543: Find the center of the circles tangent to 5x-2y-1=0 at 1,2 with a radius of 3
Found 2 solutions by MathLover1, Edwin McCravy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! If the equation of the circle is
 where ( where ( , , ) is the center, we can find the gradient by differentiation: ) is the center, we can find the gradient by differentiation:

At ( , , ) the gradient ) the gradient  is given by is given by

Therefore 
Point ( , , ) lies on the circle: ) lies on the circle:

The gradient of the line  is given by is given by
 : : 

This gradient is tangent to the circle, so




So,










 =± =±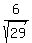
 = = ± ±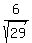
 = =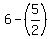 ( ( ± ±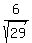 )= )= ± ± = = ± ±
So we have two circles with different centers:
( , ,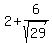 ) and ( ) and (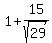 , ,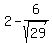 ) )
or approximately
( , ,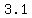 ) and ( ) and (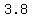 , , 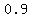 ) )
equations:

and


Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the center of the circle be (h,k).
  The red line is the given line
5x-2y-1 = 0. The green line is the line perpendicular to it.
Since 5x-2y-1 = 0 solved for y is
The red line is the given line
5x-2y-1 = 0. The green line is the line perpendicular to it.
Since 5x-2y-1 = 0 solved for y is  , its slope
is , its slope
is  so the green line has slope so the green line has slope 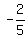 and since it
goes through (1,2) we use the point slope formula and get the equation: and since it
goes through (1,2) we use the point slope formula and get the equation:




 <-- equation of green line.
Since (h,k) lies on the green line, <-- equation of green line.
Since (h,k) lies on the green line,
 Next we use the formula for the distance from a point (x1,y1) to the line
Ax+By+C=0, which is
Next we use the formula for the distance from a point (x1,y1) to the line
Ax+By+C=0, which is
 and the distance from (h,k) must be ±3 units to the line 5x-2y-1=0, so we have
and the distance from (h,k) must be ±3 units to the line 5x-2y-1=0, so we have



 We solve the system:
We solve the system:
 using the + and then the -, the two centers are
(h,k) = (-1.785439973,3.114172029)
and
(h,k) = (3.785430073,0.8858279709)
Edwin
using the + and then the -, the two centers are
(h,k) = (-1.785439973,3.114172029)
and
(h,k) = (3.785430073,0.8858279709)
Edwin
|
|
|