Question 1136733: If the sums of the first three terms of an AP and a GP are equal and non-zero, the common difference of the AP and the common ratio of the GP are equal and the ratio of the AM to the GM is 1:-2, find the common ratio of the GP. Also, find the relationship between their first terms.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source):
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
AM is the standard abbreviation for "Arithmetic Mean".
GM is the standard abbreviation for "Geometric Mean".
So, almost everything is clear, except one thing: When the condition says "the ratio of the AM to the GM is 1:-2"
it missed to say to which progressions these AM and GM do relate.
So, it requires some interpretation; therefore I will re-edit the problem in this way:
The sums of the first three terms of an AP and a GP are equal and non-zero,
the common difference of the AP and the common ratio of the GP are equal,
and the ratio of the AM of AP to the GM of GP is 1:-2.
Find the common ratio of the GP.
by underlying my insertions.
Solution
Since this problem, although elementary, is a bit higher than the average School Math level, I will assume that the reader's
level does correspond to the problem level, and will not explain elementary details.
Let " a " be the middle (the second) term of the AP and " b " is the middle (the second) term of the GP.
Then it is widely known that AM of the first three terms of an AP is equal to "a",
while the GM of the first three terms of an GP is equal to "b".
Therefore this statement of the condition "the ratio of the AM of AP to the GM of GP is 1:-2" simply means that
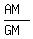 =  =  . (1)
Let "r" be the common difference of the AP and the common ratio of the GP (they are equal, so I use one symbol for both).
Then the fact that "The sums of the first three terms of an AP and a GP are equal"
gives the second equation
3a =  + b +  . (2)
From equation (1), express b = -2a and substitute it into equation (2). You will get
3a = 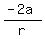 - 2a - (2a)*r.
Cancel factor "a" in both sides
3 =  - 2 - 2r;
Multiply by "r" both sides
3r = - 2 - 2r - 2r^2
and write the quadratic equation in the standard form
2r^2 + 5r + 2 = 0.
Quadratic formula gives the roots r = -2 and r = .
So, the common difference of the AP may have these two values,
and the common difference of the GP may have these two values, RESPECTIVELY.
Having these solutions for "r", we can make one step forward and find "the relationship between first terms of the AP and GP".
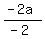a) If a = r = -2, then  = a - r = a - 2;  =  = substitute here b = -2a from above =  = a.
Therefore, = a = + 2 is that relationship between and in this case.
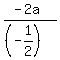b) If a = r = , then = a - r = a +  ; =  = substitute here b = -2a from above =  = 4a.
Therefore, = 4a =  - 2 is that relationship between and in this case.
ANSWER. There are two possibilities: a) r = -2 and = + 2; and
b) r = and = -2.
Solved.
|
|
|
