SOLUTION: The Jurassic Zoo charges ​$9 for each adult admission and ​$7 for each child. The total bill for the 119 people from a school trip was ​$885. How many adults and how many chi

    Number of adults = 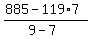 = 26.  The rest  119-27 = 92 are children.



Explanation to the one line solution


Let's assume for a minute that all tickets are children.

Then the revenue would be 119*7 = 883 dollars.

But in reality the revenue is 885 dollars.

The difference of  (885 - 833) = 52 dollars is due to our assumption that all tickets are children.


So, we should replace some number of children tickets by adult tickets.

At each replacement, we diminish the difference of $52 by 2 dollars - 

    hence, the number of adult tickets is exactly 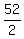 = 26 = .

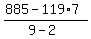Exactly as the "one line solution formula" predicts.

    x +  y = 119       (1)    (counting people)

   7x + 9y = 885       (2)    (counting dollars)


Apply the Elimination method. For it, multiply eq(1) by 7 (both sides). Keep eq(2) as is.


   7x + 7y = 119*7     (1')    

   7x + 9y = 885       (2')    


Subtract eq(1') from eq(2'). You will get

         9y - 7y = 885 - 119*7

         2y      = 885 - 119*7

          y  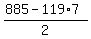    =  = 26.    (3)


We got the same answer: 26 adults.


Notice that the formula (3) is the same as the "one line solution" formula.

    a)  One line solution with the explanation on how and why it works.
        You can apply this logic solution method to many other problems.


    b)  Algebra solution with the "two equations setup".

     
    c)  The Elimination method to solve the system of 2 equations in 2 unknowns.


    d)  The proof that the two methods a) and b) give the same result and produce the same solution formula.