.
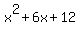 =
= 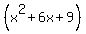 + 3 =
+ 3 = 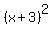 + 3.
So, this expression is the sum of two terms.
First term is quadratic binomial
+ 3.
So, this expression is the sum of two terms.
First term is quadratic binomial 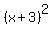 , which ALWAYS is non-negative as a square of a real number.
The second term is constant term "3", which is positive, too.
Therefore, their sum is ALWAYS positive.
Thus, the original expression is always positive, too.
, which ALWAYS is non-negative as a square of a real number.
The second term is constant term "3", which is positive, too.
Therefore, their sum is ALWAYS positive.
Thus, the original expression is always positive, too.
--------------
It is a TEMPLATE and a SAMPLE to you on how this and similar problems should be solved and worded.
The method which I used is called "completing the square".
On how this method works, you can read from the lesson
- HOW TO complete the square - Learning by examples
in this site.
/\/\/\/\/\/\/\/
Do not forget to post your "Thanks" to me after completing reading my post.