Question 112533: im not sure if this is the topic for it but how do you find or do standard form with integer coefficients?
what are coefficients? how do you find them?
example......
-4y + 6x + 7 = 0
y= -11x -4
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! In mathematics, a coefficient is a constant multiplicative factor of a certain object. The object can be such things as a variable, a vector, a function, etc. For example, the coefficient in  is 9. is 9.
Integer coefficients are simply coefficients that are integers.
The standard form of a linear equation in two variables is  , the standard for of a linear equation in n variables is , the standard for of a linear equation in n variables is 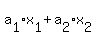 +...+ +...+
If you had a mess like this:  and you wanted to put it in standard form with integer coefficients, then you would first put the terms in order, like this: and you wanted to put it in standard form with integer coefficients, then you would first put the terms in order, like this:
 (by adding (by adding 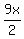 to both sides) to both sides)
And then get rid of that pesky 2 in the x term coefficient denominator by multiplying both sides of the equation by 2, thus:
 . Et Voila! By the way, the x-term coefficient in the original problem I just posed is . Et Voila! By the way, the x-term coefficient in the original problem I just posed is  , because , because 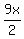 is the same thing as is the same thing as 
One more thing that is perhaps not obvious. If you have a simple variable, such as x in an equation, the coefficient is understood to be 1. We generally don't bother to write 1x, although it wouldn't necessarily be incorrect to do so. So in the second example that you provided the coefficient on the y term is 1.
Also, if there is no variable, like the 7 in your first example, or the -4 in your second example, the 7 and the -4 are refered to as the constant coefficients.
Ok, your turn. Tell me the coefficients in  . Super-double-plus-extra credit: Tell me the coefficient on . Super-double-plus-extra credit: Tell me the coefficient on  . .
Hope this helps.
John
|
|
|