SOLUTION: x −2y ≥ 0, 2x−y ≤−2, x≥0,y ≥0 solve graphically

Algebra ->  Graphs -> SOLUTION: x −2y ≥ 0, 2x−y ≤−2, x≥0,y ≥0 solve graphically      Log On


   

Question 1120283: x −2y ≥ 0, 2x−y ≤−2, x≥0,y ≥0 solve graphically
Found 3 solutions by Boreal, ikleyn, greenestamps:
Answer by Boreal(15235) About Me  (Show Source):
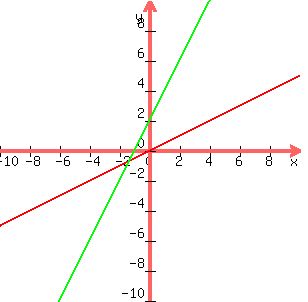
You can put this solution on YOUR website!
x-2y> =0
This is -2y>=-x or y <=(1/2)x
The second is -y <=-2x-2 or y >=2x+2
For the first, which goes through the origin, y is BELOW the graph
For the second, at (0, 0) is NOT a solution since 0 is not >=2, so the side AWAY from the origin is what is desired.
What is desired is the sector that lies wholly in quadrant III.
graph%28300%2C300%2C-10%2C10%2C-10%2C10%2C%28x%2F2%29%2C2x%2B2%29

Answer by ikleyn(52780) About Me  (Show Source):
You can put this solution on YOUR website!
.
The given system of inequalities is equivalent to 


    y <= x%2F2               (1)

    y >= 2x + 2           (2)

    x >= 0,  y >= 0       (3)


The plot below represents line (1) in red and line (2) in green.






Plot y = x%2F2 (red) and y = 2x+2 (green).



The solution to inequality (1) is the set of all points belonging to the half plane on and below the red line (including points of this line).

The solution to inequality (2) is the set of all points belonging to the half plane on and highlight%28cross%28below%29%29 above the green line (including points of this line).

The solution to inequality (3) is the set of all points belonging to first quadrant QI (including points of x- and y-axes).


The solution to the given system of inequalities (1), (2) and (3) is the intersection of the sets described above.


As you can see it from the plot, this intersection is the EMPTY set  (which means that there is no point  (x,y)  
in the coordinate plane satisfying given inequalities simultaneously).


Thus the set of solution to the given system is the empty set.

In other words, the given system HAS NO solutions.


Be aware :   the solution and the answer by  @Boreal  is  I N C O R R E C T.



Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


Just a note to tutor @ikleyn....

You unintentionally said the solution to inequality (2) was the set of points below the line; clearly you meant above, making the solution the empty set....