Question 1120102: Find all values of x that satises the inequality f(x)=(2x −3)/(x −2)(x−4) < 0.
Found 3 solutions by greenestamps, ikleyn, 7022:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
I will assume that both the (x-2) and (x-4) factors are in the denominator: 
The critical points are where the numerator or denominator is zero.
The function value is zero when the numerator is zero:
2x-3 = 0 --> x = 1.5
The function value is undefined when the denominator is zero:
x-2 = 0 --> x = 2; and x-4 = 0 --> x = 4
The critical points divide the domain into intervals; you can use test points and do a sign analysis to determine whether the function value is positive or negative on each interval. An even number of negative factors means the function value is positive; an odd number means the function value is negative:
x < 1.5: 3 negative factors; function value negative
x = 1.5: function value 0
1.5 < x < 2: 2 negative factors; function value positive
x = 2: function value undefined
2 < x < 4: 1 negative factor; function value negative
x = 4: function value undefined
x > 4: 0 negative factors; function value positive
Note you can speed up the process without using test points in each interval. Simply start at one end of the number line and "walk" towards the other end, noting that the sign of the function changes each time you pass a critical point:
function value negative for large negative values of x (3 negative factors)
function value changes to positive when we pass x = 1.5
function value changes to negative when we pass x = 2
function value changes to positive when we pass x = 4
Answer: The function value is negative for x < 1.5 and for 2 < x < 4
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
First, the formula is ambiguous, since it can be read in different ways.
One way to read it is f(x) =  .
Another way is f(x) =  .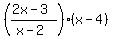
To make it UNAMBIGOUS, you must use parentheses, showing which part is the numerator, and which is the denominator.
I will read the formula f(x) = .
The critical points are x=  (the zero of the numerator and the zero of the function),
x= 2 and x= 4 (the zeroes of the denominator).
They divide the number line in four intervals
 < x < , < x < 2, 2 < x < 4 and 4 < x <  .
1. In the interval < x < all three factors (2x-3), (x-2) and (x-4) are negative.
So, the function f(x) is negative as the product/quotient of three negative numbers.
So, this interval < x < is the part of the solution domain.
2. In the interval < x < 2, the factor (2x-3) is positive, while (x-2) and (x-4) are negative.
So, the function f(x) is positive as the product/quotient of one positive and two negative numbers.
So, this interval < x < 2, is not the part of the solution domain.
3. In the interval 2 < x < 4, the factors (2x-3) and (x-2) are positive, while (x-4) is negative.
So, the function f(x) is negative as the product/quotient of two positive and one negative numbers.
So, this interval 2 < x < 4, is the part of the solution domain.
4. In the interval 4 < x, the factors (2x-3), (x-2) and (x-4) are positive.
So, the function f(x) is positive as the product/quotient of three positive numbers.
So, this interval 4 < x is not a part of the solution domain.
Answer. The solution set is the union of two intervals (,) U (2,4).
Solved.
==================
To see many other similar solved problems, look into the lessons
- Solving problems on quadratic inequalities,
- Solving inequalities for high degree polynomials factored into a product of linear binomials
- Solving inequalities for rational functions with numerator and denominator factored into a product of linear binomials
in this site.
Answer by 7022(2)  (Show Source):
You can put this solution on YOUR website! ∵ (2x-3)/(x-2)(X-4 ) < 0 Multiplying both sides by (x-2)^2 (x-4)^2
⇨ (2x-3)(x-2)(X-4 ) < 0
⇨ 1) either 2x-3 < 0 ⇨ x< 3/2
2) or (x-2)(X-4) < 0 ⇨ 2 < x < 4
From Eq 1) and 2)
S.s = (-∞ ,3/2) Ü (2,4) #
|
|
|
