|
Question 1119520: If the equations x2 −ax+b = 0 and x2−ex+f = 0haveoneroot in common and if the second equation has equal roots, then prove that ae = 2(b + f).
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If the equations x^2 - ax + b = 0 and x^2 - ex+f = 0 have one root in common and if the second equation has equal roots,
then prove that ae = 2(b + f).
~~~~~~~~~~~~~~~~~
1. If 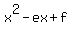 = 0 has equal roots, it means that its discriminant d = e^2 - 4f is zero: = 0 has equal roots, it means that its discriminant d = e^2 - 4f is zero:
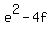 = 0, or = 0, or  = = 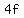 , or , or 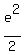 = 2f. (1)
2. Then the merged root of the equation = 2f. (1)
2. Then the merged root of the equation 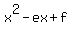 = 0 is = 0 is
 = = 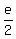 ( <<<---=== it follows from the quadratic formula, for example )
3. It implies that the common root of the two given equations is ( <<<---=== it follows from the quadratic formula, for example )
3. It implies that the common root of the two given equations is 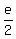 , since the second equation has no other roots.
4. Thus we know that , since the second equation has no other roots.
4. Thus we know that 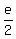 is one of the roots of the equation is one of the roots of the equation 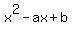 = 0.
Then, according to the Vieta's theorem, the other root of this equation is = 0.
Then, according to the Vieta's theorem, the other root of this equation is
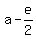 , and the product of the roots is the constant term , and the product of the roots is the constant term
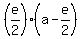 = b.
5. The last equality is equivalent to = b.
5. The last equality is equivalent to
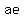 - - 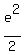 = 2b <-----> ae = = 2b <-----> ae = 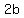 + + 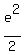 <-----> ae = 2b + 2f <-----> ae = 2(b+f).
The transformation step before the last one uses the equality (1). <-----> ae = 2b + 2f <-----> ae = 2(b+f).
The transformation step before the last one uses the equality (1).
It is what has to be proved.
-------------
The Vieta's theorem is fantastically powerful and effective tool in solving such problems.
And those who have it in their hands and their minds, are half head higher in Math competitions than those who have not.
For other solved problems with the use of the Vieta's theorem see the lesson
- Using Vieta's theorem to solve qudratic equations and related problems
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this textbook under the topic "Quadratic equations".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
=============
I remember your previous post in this forum
https://www.algebra.com/algebra/homework/Graphs/Graphs.faq.question.1119502.html
which I asked you to separate into different posts.
Now imagine for a minute that in response to your original post you obtain an answer of 10 times of this size.
You would simply loose yourself in this writing.
It is why the rule requires separate posts for separate problems.
|
|
|
| |