Question 1119428: Without the derivative find the value of minima of
(x+1)(x+2)(x+3)(x+4)
Found 2 solutions by Shin123, ikleyn:
Answer by Shin123(626)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let me introduce new variable u = x+2.5.
Then x+2 = u-0.5, x+3 = u+0.5 and (x+2)*(x+3) = (u-0.5)*(u+0.5) =  .
Similarly, x+1 = u-1.5, x+4 = u+1.5 and (x+1)*(x+4) = (u-1.5)*(u+1.5) = .
Similarly, x+1 = u-1.5, x+4 = u+1.5 and (x+1)*(x+4) = (u-1.5)*(u+1.5) =  .
And the product (x+1)(x+2)(x+3)(x+4) is .
And the product (x+1)(x+2)(x+3)(x+4) is  .
Thus we have two quantities r = .
Thus we have two quantities r =  and s = and s =  , such that their difference (r - s) has the constant value of 2
r - s = , such that their difference (r - s) has the constant value of 2
r - s =  - - 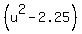 = 2, (1)
and we are looking for the minimum value of the product r*s.
From (1), r = 2+s, so we are looking for the minimum of the quadratic function
r*s = (2+s)*s = = 2, (1)
and we are looking for the minimum value of the product r*s.
From (1), r = 2+s, so we are looking for the minimum of the quadratic function
r*s = (2+s)*s = 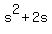 .
The minimum is EXACTLY at the MIDPOINT BETWEEN the ZEROES s= 0 and s= -2, i.e. at s= -1.
s= -1 means u^2 - 2.25 = -1, or u^2 = -1 + 2.25 = 1.25,
which, in turn, means .
The minimum is EXACTLY at the MIDPOINT BETWEEN the ZEROES s= 0 and s= -2, i.e. at s= -1.
s= -1 means u^2 - 2.25 = -1, or u^2 = -1 + 2.25 = 1.25,
which, in turn, means 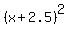 = 1.25 ====> x = -2.5 +- = 1.25 ====> x = -2.5 +-  .
Thus we found two minimums for the original function y(x) = (x+1)(x+2)(x+3)(x+4).
These minimums are .
Thus we found two minimums for the original function y(x) = (x+1)(x+2)(x+3)(x+4).
These minimums are  = -2.5 - = -2.5 -  = -3.62 (approximately), and = -3.62 (approximately), and
 = -2.5 + = -2.5 +  = -1.38 (approximately).
The plot below visually confirms this answer. = -1.38 (approximately).
The plot below visually confirms this answer.
 Plot y = (x+1)(x+2)(x+3)(x+4)
The Table below (obtained with MS Excel) also confirms the answer.
x y(x)
------------------------------------
-3.9 -0.4959
-3.8 -0.8064
-3.7 -0.9639
-3.6 -0.9984 (*) -3.618033989
-3.5 -0.9375
-3.4 -0.8064
-3.3 -0.6279
-3.2 -0.4224
-3.1 -0.2079
-3 0.0000
-2.9 0.1881
-2.8 0.3456
-2.7 0.4641
-2.6 0.5376
-2.5 0.5625
-2.4 0.5376
-2.3 0.4641
-2.2 0.3456
-2.1 0.1881
-2 0.0000
-1.9 -0.2079
-1.8 -0.4224
-1.7 -0.6279
-1.6 -0.8064
-1.5 -0.9375
-1.4 -0.9984 (*) -1.381966011
-1.3 -0.9639
-1.2 -0.8064
-1.1 -0.4959
-1 0.0000
-0.9 0.7161
-0.8 1.6896
-0.7 2.9601
-0.6 4.5696
-0.5 6.5625
-0.4 8.9856
-0.3 11.8881
-0.2 15.3216
-0.1 19.3401
If you want to get the values of minimums, you can take them from the table.
These values both are equal to -0.9984 (approximately).
Plot y = (x+1)(x+2)(x+3)(x+4)
The Table below (obtained with MS Excel) also confirms the answer.
x y(x)
------------------------------------
-3.9 -0.4959
-3.8 -0.8064
-3.7 -0.9639
-3.6 -0.9984 (*) -3.618033989
-3.5 -0.9375
-3.4 -0.8064
-3.3 -0.6279
-3.2 -0.4224
-3.1 -0.2079
-3 0.0000
-2.9 0.1881
-2.8 0.3456
-2.7 0.4641
-2.6 0.5376
-2.5 0.5625
-2.4 0.5376
-2.3 0.4641
-2.2 0.3456
-2.1 0.1881
-2 0.0000
-1.9 -0.2079
-1.8 -0.4224
-1.7 -0.6279
-1.6 -0.8064
-1.5 -0.9375
-1.4 -0.9984 (*) -1.381966011
-1.3 -0.9639
-1.2 -0.8064
-1.1 -0.4959
-1 0.0000
-0.9 0.7161
-0.8 1.6896
-0.7 2.9601
-0.6 4.5696
-0.5 6.5625
-0.4 8.9856
-0.3 11.8881
-0.2 15.3216
-0.1 19.3401
If you want to get the values of minimums, you can take them from the table.
These values both are equal to -0.9984 (approximately).
Solved.
|
|
|