SOLUTION: Find f(7)+f^-1(7) if f(3x-2)=x+5

Algebra ->  Graphs -> SOLUTION: Find f(7)+f^-1(7) if f(3x-2)=x+5       Log On


   

Question 1118646: Find f(7)+f^-1(7) if f(3x-2)=x+5
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


I don't know a formal way for finding f(x) from the given information. Perhaps another tutor will also respond with a different method than I use.

For me, f(3x-2) = x+5 means that f(x) is of the form f%28x%29+=+%28x%2F3%29%2Bb.

To find b, use the given fact that f(3x-2) = x+5:

f%283x-2%29+=+%283x-2%29%2F3+%2B+b+=+x%2B5
x-2%2F3%2Bb+=+x%2B5
b+=+5%2B2%2F3+=+17%2F3

So

f%28x%29+=+%28x%2F3%29%2B17%2F3

Then

f%287%29+=+7%2F3+%2B+17%2F3+=+24%2F3+=+8

To find f^-1(7), set f(x)=7 and solve for x:

7+=+%28x%2F3%29%2B17%2F3
4%2F3+=+x%2F3
x+=+4

Finally, then, f(7)+f^-1(7) = 8+4 = 12.

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
One possible solution 

(1)  To calculate f(7), you need to find a value of x such that 3x-2 = 7.


     You can do it in one line:  3x-2 = 7  ====>  3x = 7+2 = 9  ====>  x = 9/3 = 3.


     Then f(7) = f(3*3-2) = 3 + 5 = 8,  according the given definition of the function f.




(2)  To find  f%5E%28-1%29%287%29,  you first find "x" from equation x+5 = 7  (left side of the definition of the function f).


     You do it in one line:  x = 7-5 = 2.


     Then you calculate  3x-2  at  x= 2,  and you get  the value  3*2-2 = 6-2 = 4.


     So, f(4) = 7,  which implies   f%5E%28-1%29%287%29 = 4.




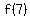(3)  Finally,  f%287%29 + f%5E%28-1%29%287%29 = 8 + 4 = 12.


Other possible solution 

(1)  You are given  f(3x-2) = x + 5.


    Introduce new variable  t = 3x-2   and  express  x  via t.


    You will get  x = 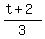%28t%2B2%29%2F3.


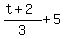    Thus  f(t) = x + 5 = %28t%2B2%29%2F3+%2B+5     (*)

        is the expression (definition) of the given function as the function of "t".


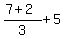     Now  f(7) = %287%2B2%29%2F3%2B5 = 9%2F3%2B5 = 3 + 5 = 8.



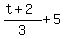(2)  To find  f%5E%28-1%29%287%29,  you need to find which number "t" gives the value of 7 to the expression  %28t%2B2%29%2F3+%2B+5, which is left side of (*).


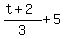     So, you solve the equation  %28t%2B2%29%2F3+%2B+5 = 7,

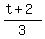     and you do it in one line  %28t%2B2%29%2F3 = 7 - 5 = 2  ====>  t+2 = 3*2  ====>  t = 3*2 -2 = 4.


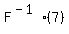     Thus,  F%5E%28-1%29%287%29 = 4,  and you get the same answer as in the first solution above:



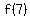     f%287%29 + f%5E%28-1%29%287%29 = 8 + 4 = 12.

Solved completely in two ways.