.
Let me introduce new variable u =  .
Then I can reformulate the problem in this EQUIVALENT way:
If
.
Then I can reformulate the problem in this EQUIVALENT way:
If 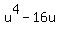 =
=  , then find
, then find 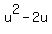 .
.
Solution
If 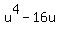 =
=  , then
, then
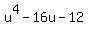 = 0. (1)
The left side can be factored:
= 0. (1)
The left side can be factored:
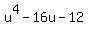 =
= 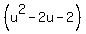 .
. into the product of two quadratic polynomials. (You may check the validity of this decomposition on your own).
Thus the equation (1) is equivalent to
into the product of two quadratic polynomials. (You may check the validity of this decomposition on your own).
Thus the equation (1) is equivalent to
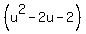 .
. = 0. (2)
If "u" is the real root of the equation (1), then "u" is the real root of the equation (2).
But the second polynomial (second multiplier)
= 0. (2)
If "u" is the real root of the equation (1), then "u" is the real root of the equation (2).
But the second polynomial (second multiplier)  is positively defined quadratic function
is positively defined quadratic function 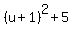 , which has NO real roots.
Therefore, "u" is the root of the first trinomial of (2), i.e.
, which has NO real roots.
Therefore, "u" is the root of the first trinomial of (2), i.e.
 = 0,
Then
= 0,
Then  =
= 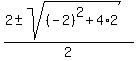 =
= 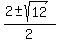 =
= 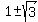 .
Now, if
.
Now, if  =
= 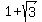 , then
, then  =
= 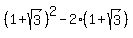 =
=  = 2.
If
= 2.
If  =
=  , then
, then  =
=  =
=  = 2.
Thus in any case
= 2.
Thus in any case  = 2.
It is the answer to the problem question.
Answer. If x is a real number such as
= 2.
It is the answer to the problem question.
Answer. If x is a real number such as  =
=  , then
, then  = 2.
= 2.
Solved.