SOLUTION: Tommy and Zach are starting out at the same position. Tommy runs north at 3 miles per hour and Zach starts to run east 2 hours later at the rate of 4 miles per hour. How long until

Algebra ->  Graphs -> SOLUTION: Tommy and Zach are starting out at the same position. Tommy runs north at 3 miles per hour and Zach starts to run east 2 hours later at the rate of 4 miles per hour. How long until      Log On


   

Question 1113901: Tommy and Zach are starting out at the same position. Tommy runs north at 3 miles per hour and Zach starts to run east 2 hours later at the rate of 4 miles per hour. How long until Tommy and Zach are 8 miles apart?


Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
The distance between them is the hypotenuse of a right-angled triangle with the legs of  3t miles  and  4(t-2) miles:


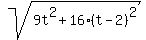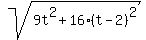D = sqrt%289t%5E2+%2B+16%2A%28t-2%29%5E2%29.


The problem asks to find "t" such as


sqrt%289t%5E2+%2B+16%2A%28t-2%29%5E2%29 = 8,   or,  equivalently,  9t^2 + 16*(t-2)^2 = 64.


9t^2 + 16t^2 - 64t + 64 = 64


25t^2 = 64t   ====>  the only answer is  t = 64/25 of an hour  after Tommy started his run,  or  0.56 of an hour = 33.6 minutes  after Zach  started his run.