Question 1113593: find three consecutive odd integers such that twice the largest increased by 4 times the smallest is not less than 20 less than nine times the middle.
Found 2 solutions by KMST, MathTherapy:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the integers be
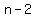 , ,  , and , and  . .
We can eliminate any even answers later.
We calculate that
"twice the largest" =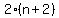 , ,
"4 times the smallest" =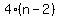 , ,
"twice the largest increased by 4 times the smallest" = 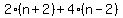 , ,
and "20 less than nine times the middle" =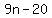 . .
The problem, says that 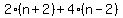 "is not less than" "is not less than"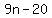 . .
Because it has to be either one way or the other,
the phrase "not less than" means "more than or equal to",
so the inequality to solve is
 . .
Solving:







 , along with the fact that , along with the fact that
 and and 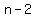 are supposed to be (positive) odd integers, are supposed to be (positive) odd integers,
means that  or or  . .
So, the "three consecutive odd integers" in the problem are
 or or 
Answer by MathTherapy(10559)   (Show Source): (Show Source):
You can put this solution on YOUR website!
find three consecutive odd integers such that twice the largest increased by 4 times the smallest is not less than 20 less than nine times the middle.
It's any 3 CONSECUTIVE ODD INTEGERS, as long as the SMALLEST <= 3.
|
|
|