.
If 1/x+1/y =-1, x^3 + y^3 = 4 find x & y
~~~~~~~~~~~~~~~~~~~~~~~~~~
1.  +
+  = -1 ====> x + y = - xy (1)
2.
= -1 ====> x + y = - xy (1)
2.  +
+  = 4 ====>
= 4 ====>
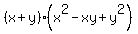 = 4. (2)
In (2), replace (x+y) by -xy and replace (x^2 - xy + y^2) by
= 4. (2)
In (2), replace (x+y) by -xy and replace (x^2 - xy + y^2) by  =
= 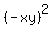 -
- 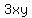 , based on (1).
You will get instead of (2)
, based on (1).
You will get instead of (2)
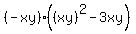 = 4. (3)
Let t = xy be new variable. Then (3) becomes
-t*(t^2 -3t) = 4,
t^3 - 3t^2 + 4 = 0. (4)
It is easy to check that t= -1 and t= 2 are the roots to (4).
So, from the two original equations we have two and only two possibilities for xy
xy = -1 OR xy = 2.
3. Thus the original system of two equations (one of which is of the degree 3 !)
deploys in two systems of much simpler equations:
a) x + y = 1
xy = -1
which implies x*(1-x) = -1 ====> x*(x-1) = 1 ====> x^2 -x - 1 = 0 ====>
= 4. (3)
Let t = xy be new variable. Then (3) becomes
-t*(t^2 -3t) = 4,
t^3 - 3t^2 + 4 = 0. (4)
It is easy to check that t= -1 and t= 2 are the roots to (4).
So, from the two original equations we have two and only two possibilities for xy
xy = -1 OR xy = 2.
3. Thus the original system of two equations (one of which is of the degree 3 !)
deploys in two systems of much simpler equations:
a) x + y = 1
xy = -1
which implies x*(1-x) = -1 ====> x*(x-1) = 1 ====> x^2 -x - 1 = 0 ====>  =
=  =
=  OR
b) x + y = -2
xy = 2
which implies x*(-2-x) = 2 ====> x*(x+2) = -2 ====> x^2 +2x + 2 = 0 ====>
OR
b) x + y = -2
xy = 2
which implies x*(-2-x) = 2 ====> x*(x+2) = -2 ====> x^2 +2x + 2 = 0 ====>  =
= 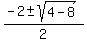 =
= 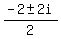 =
=  .
Answer. There are 4 solutions: two real (x,y) = (
.
Answer. There are 4 solutions: two real (x,y) = ( 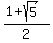 ,
, 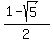 ), (x,y) = (
), (x,y) = ( 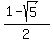 ,
, 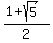 ),
and two complex (x,y) = (
),
and two complex (x,y) = ( 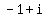 ,
, 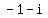 ), (x,y) = (
), (x,y) = ( 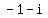 ,
, 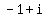 ).
).