Question 1109882: solve : (ln(1+4/x)) ^2 +(ln(1-4/(x+4)))^2 =2(ln((3-x)/(x-1)))^2
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The equation has a few restrictions, but we can worry about it later,
as we may have to get rid of some extraneous solutions, anyway.
For now, we will assume  , , 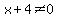 , etc. , etc.
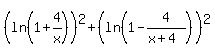  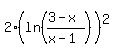
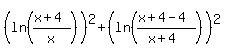  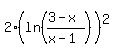
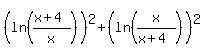  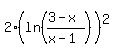
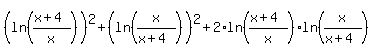  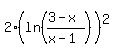
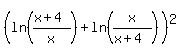  
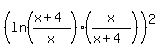  
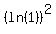  
  
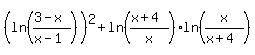  
  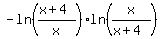
  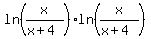
  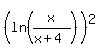
If both logarithms have the same sign (both positive or both negative,
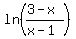   <--> <--> 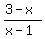  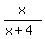 . .
Otherwise,
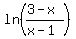  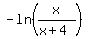 <--> <--> 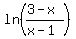  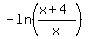 <--> <--> 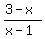  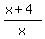 . .
And we trudge on.
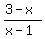  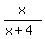
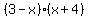  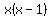





For  , ,
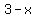 , ,  , ,  , ,  , , 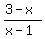 , and , and 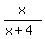 are all positive, are all positive,
so it looks like a valid solution, and it verifies.
For  , , 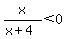 , ,
so  does not exist/is undefined, does not exist/is undefined,
so we know  is not a solution. is not a solution.
I do not have to try to verify that.
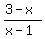  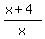
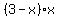  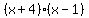





For  , ,
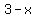 , ,  , ,  , ,  , , 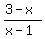 , and , and 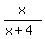 are all positive, are all positive,
so it looks like a valid solution, and it verifies.
For  , , 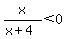 , ,
so  does not exist/is undefined, does not exist/is undefined,
so we know  is not a solution. is not a solution.
I do not have to try to verify that.
HOW WE VERIFY:
For 
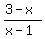  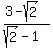  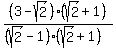  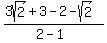  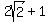
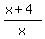  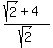  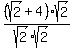  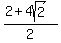  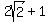
|
|
|