|
Question 110005: find the length of a radius of the circle x^2+y^2-4x-6y-5=0
Found 2 solutions by elima, bucky:
Answer by elima(1433)   (Show Source):
Answer by bucky(2189) (Show Source):
You can put this solution on YOUR website! Given the equation:
.
.
We need to get this into the standard form for the equation of a circle. Begin by getting rid
of the -5 on the left side. You can do this by adding +5 to both sides so that you get:
.
.
Next collect the x terms and the y terms on the left side. When you do that the equation becomes:
.
.
Next complete the square for each of the two quantities inside the parentheses. For the first
quantity you will complete the square of 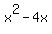 . Because the coefficient (multiplier) of
the  term is one, you can find what has to be added to complete the square by using
the following method. Divide the multiplier of the x term by 2 and square the result. This
means that you divide -4 by 2 and get -2. Then square the -2 to get +4. So you need to add
+4 inside the parentheses. But if you add +4 to the left side of the equation, you must also
add +4 to the right side. This means the equation becomes:
.
.
The polynomial inside the first set of parentheses is now a perfect square, and you can write
it as such. On the right side the 5 and the +4 can be added to get 9. This makes the
equation become:
.
.
Next you do the same thing for the y-terms in the second set of parentheses. Since the
coefficient of the y^2 term is 1, you can find the number you need to add in this second
set of parentheses to form a perfect square. Take half the coefficient of the y term, that is,
take half of -6 to get -3 and square this to get +9. Therefore, by adding 9 inside these
parentheses you get a perfect square. And if you add 9 on the left side you must also add 9 on
the right side of the equation. Doing both of these actions results in:
.
.
Next write the polynomial in the second set of parentheses as a perfect square and also add the
two 9s on the right side to get 18. When you do these two things, the equation becomes:
.
.
This is the standard form of an equation of a circle. In this case, the center of the circle
is located at the point (2, 3) and the radius of the circle is the square root of the right
side ... or  .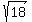
.
The radius can be simplified by applying some laws of square roots. In particular:
.
.
So that is the answer ... the radius of the circle is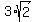 
.
Hope this is understandable to you. It will help if you relate this to an explanation in
a textbook so you get more of a feel for what is going on ... Please verify the math to
make sure that I didn't make a sign error or some other simple mistake in doing this work.
.
|
|
|
| |
