.
Substitute y = mx+5 into the circle equation. You will get
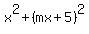 = 10,
= 10,
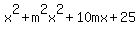 = 10,
= 10,
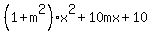 = 0. (1)
The condition that the straight line is tangent to the circle is equivalent to the fact that the equation (1) has only one root,
which, in turn, means that the discriminant of the equation (1) is equal to zero.
It gives you an equation for m:
d =
= 0. (1)
The condition that the straight line is tangent to the circle is equivalent to the fact that the equation (1) has only one root,
which, in turn, means that the discriminant of the equation (1) is equal to zero.
It gives you an equation for m:
d = 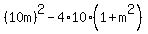 = 0.
Simplify and solve it for m:
= 0.
Simplify and solve it for m:
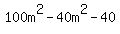 = 0,
= 0,
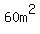 = 40 ====>
= 40 ====> 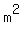 =
=  =
=  ====> m = +/-
====> m = +/- 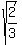 .
.
Solved.
The lesson to learn from this solution:
The fact that a line is tangent to the circle is equivalent to the fact that they have only one common point.