Question 1071484: Find the slope of the line through (8, 2) and (6, 6).
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The slope,  is is

If you need a formula:
The slope of the line through 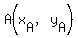 and and 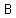 is is
 . .
If you need a tip:
1) To make sure you do not get numbers mixed up,
start with   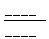 . .
2) Pick one of the points (it does not matter, and write its coordinates in,
y on top, x in the bottom, each followed with a minus sign,
to get something like
   . .
3) fill the blanks with the coordinates of the other point,
y on top, x in the bottom, to get something like
   . .
If you need understanding:
The slope means the rate of increase in the y-coordinate,
meaning
the increase in y-coordinate per unit increase of the x-coordinate.
When going from (6,6) to (8,2) , x increases from 6 to 8,
an increase of  . .
At the same time y changes from 6 to 2,
an increase of  , ,
which you may want to call a decrease of 4.
Since a straight line has the same slope throughout,
an increase of  in in  as as  increases by increases by  , ,
means that for every unit increase in x, the increase in y is  , ,
the ratio of y increase to x increase,  . .
|
|
|