SOLUTION: x=y+2 2x+y=1

x = y+2,     (1)
2x+y = 1.    (2)


To solve this system, apply the Substitution method.
You just have "x" expressed via "y" in the equation (1).
Substitute it into the equation (2). Ypou will get

2*(y+2) + y = 1.

It is a single equation for "y". You just excluded "x".

Solve th equation (3) for "y":

2y + 4 + y =1,

3y = 1 - 4,

3y = -3,

y = 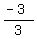 = -1.

Thus you just found y. It is 1.

Now from (1) find x = y+2 = -1+2 = 1.

Answer.  x = 1,  y = -1.

Check it on your own.