SOLUTION: if f(x^2 +1)=x^4+5x^2+3. what is f(x^2 -1)

Algebra ->  Graphs -> SOLUTION: if f(x^2 +1)=x^4+5x^2+3. what is f(x^2 -1)      Log On


   

Question 1048295: if f(x^2 +1)=x^4+5x^2+3. what is f(x^2 -1)
Found 2 solutions by robertb, ikleyn:
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
f%28x%5E2+%2B1%29=x%5E4%2B5x%5E2%2B3
Let x+=+sqrt%28x-1%29.
===> .
===> f%28x%5E2+-+1%29+=+%28x%5E2+-+1%29%5E2%2B3%2A%28x%5E2+-+1%29+-+1,
do the rest...it will be good for you...

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
if f(x^2 +1)=x^4+5x^2+3. what is f(x^2 -1)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

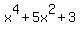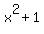My goal now is to present the polynomial in the right side,  x%5E4+%2B5x%5E2+%2B3,  as a function (as a polynomial) of the argument  x%5E2%2B1.  
We have

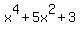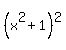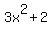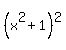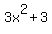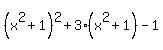x%5E4+%2B5x%5E2+%2B3 = %28x%5E2%2B1%29%5E2 + 3x%5E2+%2B+2 = %28x%5E2%2B1%29%5E2 + 3x%5E2+%2B+3 -  1 = %28x%5E2%2B1%29%5E2+%2B+3%2A%28x%5E2%2B1%29+-1.


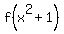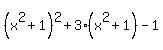Thus  f%28x%5E2+%2B1%29 = %28x%5E2%2B1%29%5E2+%2B+3%2A%28x%5E2%2B1%29+-1.

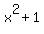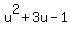      So, if I introduce new variable u = x%5E2%2B1, then f(u) = u%5E2+%2B+3u+-1.


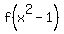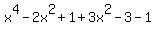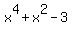Therefore, f%28x%5E2-1%29 = %28x%5E2-1%29%5E2+%2B+3%28x%5E2-1%29+-1 = x%5E4+-+2x%5E2+%2B+1+%2B+3x%5E2+-+3+-1 = x%5E4+%2B+x%5E2+-3.

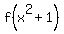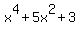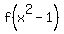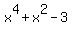Answer.  If  f%28x%5E2+%2B1%29 = x%5E4%2B5x%5E2%2B3,  then  f%28x%5E2-1%29 = %28x%5E2-1%29%5E2+%2B+3%28x%5E2-1%29+-1 = x%5E4+%2B+x%5E2+-3.