Question 1016849: The sum of the lengths of any two sides of a triangle must be greater than the third side. If a triangle has one side that is 17 inches and a second side that is 1 inch less than twice the third side, what are the possible lengths for the second and third sides?
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let  , and , and 
Case 1: 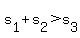 doesn't give any insight, since it reduces to doesn't give any insight, since it reduces to 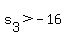 , which is always true. , which is always true.
Case 2: 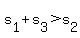 will lead, upon the proper substitution, to will lead, upon the proper substitution, to 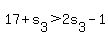 , or , or 
Case 3: 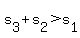 leads to leads to 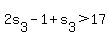 , or , or
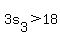 , or , or 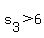
Hence, 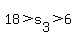 . .
Now  , and so substitution into the last inequality and simplifying yields , and so substitution into the last inequality and simplifying yields
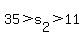 . .
|
|
|