|
Question 1014713: 5.9
Graph the solution set of the system of inequalities
x+4y<8
y>x-3
I have the graph but I wanted to make sure it's correct
Found 2 solutions by Fombitz, Theo:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! here's the graph that i made.
look below the graph for further comments.
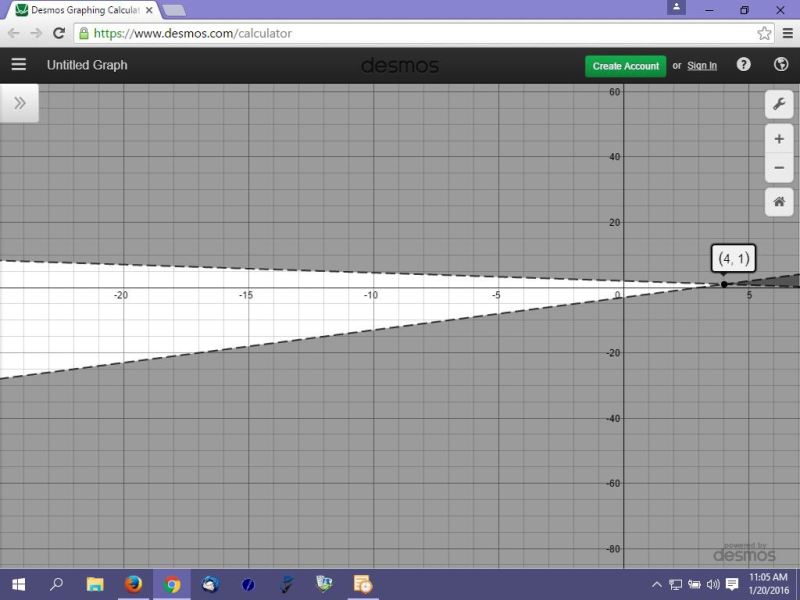
your equations are:
x+4y<8
y>x-3
in the first equation, solve for y to get y<(8-x)/4.
your two equations become:
y < (8-x)/4 and y > x-3.
in the graph, the top dashed line is the equation of y = (8-x) and the bottom line is the equation of y = x-3.
the white area between those 2 dashed lines is where your solution lies.
it is the area beneath the line of y = (8-x)/4 and above the line of y = (x-3).
it has to satisfy both those criteria to be within the solution set.
your solution area lies in the region defined by x < 4.
when x is equal to 4, y = x-3 becomes y = 1 and y = (8-x)/4 becomes y = (8-4)/4 which becomes y = 4/4 which becomes y = 1.
the coordinate point of (4,1) is on both lines.
since the inequality says that the value of y has to be below the line of y = (8-x)/4 and above the line of y = x-3, then that point does not satisfy the requirements because it is on the line.
all of your solutions lie in the region where x < 4.
there are no values of y that satisfy the requirements of the problem when x > 4.
for example:
when x = 10, y < (8-x)/4 becomes y < -2/4 and y > x-3 becomes y > 7
y cannot be < -2/4 and > 7 at the same time, so the requirements of the problem are not satisfied when x = 10.
when x = 5, y < (8-x)/4 becomes y < 3/4 and y > x-3 becomes y > 2.
y cannot be < 3/4 and > 2 at the same time, so the requirements of the problem are not satisfied when x = 5.
when x = 4, y < (8-x)/4 becomes y < 1 and y > x-3 becomes y > 1.
y cannot be < 1 and > 1 at the same time, so the requirements of the problem are not satisfied with x = 4.
when x = 3, y < (8-x)/4 becomes y < 5/4 and y > x-3 becomes y > 0.
y can be < 5/4 and > 0 at the same time, so the requirements of the problem are satisfied with x = 3.
you will only get valid solutions when x < 4.
|
|
|
| |