|
Question 1001902: . Take a piece of string, no more than 40 cm long, and tie the ends together to make it into a loop. Use your thumbs and fingers to make a rectangle with the string. Hold it over a piece of graph paper to make right angles (so that you can see the size of your rectangle. Use the units on your graph paper to measure the length l and width w of each rectangle. Record the measurements to the nearest tenth of a centimeter (or if your ruler only has inches, use inches for the entire exercise). Complete the first two columns in the table that follows. You will need to make five rectangles for this activity. Be sure to include rectangles where the length is greater than the width and where the width is greater than the length.
Length (l) Width (w) Area (A)
7.5 cm 3.5 cm 26.25 cm
3 cm 8 cm 24 cm
4.5 cm 6.5 cm 29.25 cm
3.5 cm 7.5 cm 26.25 cm
8.5 cm 2.5 cm 21.25 cm
3. Graph the length and area of each rectangle (length on the horizontal axis and area on the vertical axis)
6. How long is your loop of string? Write an expression for the width of any rectangle in terms of the length of your string.
My loop is 12 cm long and the string is 24 cm long
7. Write a function for the area of any rectangle in terms of the length
8. Graph the function on the same coordinate plane you used in #3.
9. Does your graph match the function exactly? If not, explain why.
10. Find the vertex of the graph of the area function in #7. What is the meaning of the vertex?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you have a length of a string.
you tie a knot to form a loop.
the length of the string in the loop is the perimeter of any rectangle you make.
your rectangle has length and it has width.
the area of the rectangle is equal to the length * the width.
the area will vary in size depeending on the length and the width.
the relationships that are involved are:
perimeter = 2 * length + 2 * width
area = length * width.
since the perimeter is the length of the string, then perimeter = 24 and the formula for perimeter becomes:
24 = 2 * length + 2 * width
from this formula, you can solve for width as follows:
start with:
24 = 2 * length + 2 * width
subtract 2 * length from both sides of the equation to get:
24 - 2 * length = 2 * width
divide both sides of the equation by 2 to get:
12 - length = width
solve for width to get:
width = 12 - length
you have now solved for the width in terms of the length.
area = length * width
replace width with 12 - length to get:
area = length * (12 - length)
you have now solved for the area in terms of the length.
to graph this equation, let y = area and let x = length.
you will get:
y = x * (12 - x)
simplify this equation to get:
y = 12x - x^2
reorder the terms in descending order of degree to get:
y = -x^2 + 12x
that's a quadratic equation that has a maximum value because the coefficient of the x^2 term is negative.
the general form of a quadratic equation is y = ax^2 + bx + c
your equation gets you:
a = -1
b = 12
the x coordinate of the maximum value of your equation is:
x = -b/2a = -12/2 = 6
when x = 6, y = -x^2 + 12x becomes y = -36 + 72 which becomes y = 36.
the maximum value of your equation is at (6,36).
since y represents the area, then the maximum area is 36.
x = 6 means the length = 6.
when the length = 6, the width is also equal to 6.
you can see this from the table.
here's the graph of your equation.
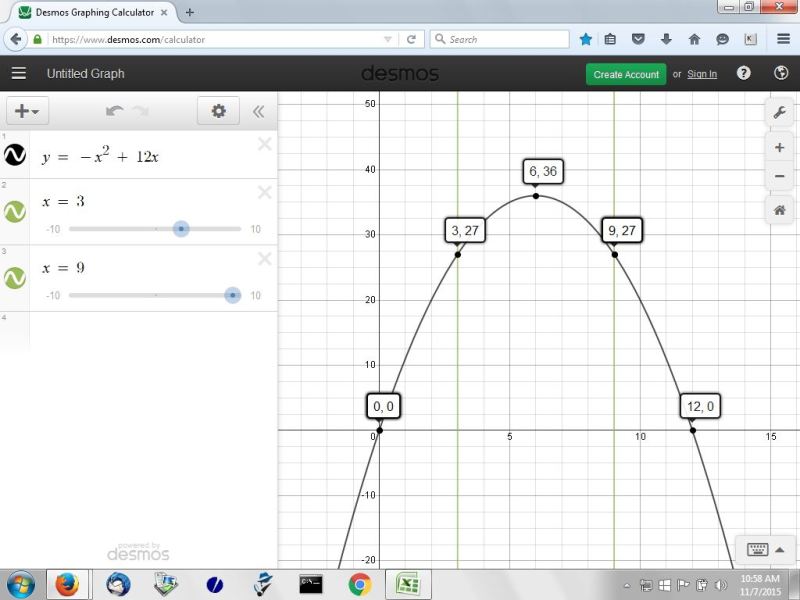
here's the table that was used to generate values that will be consistent with the graph.
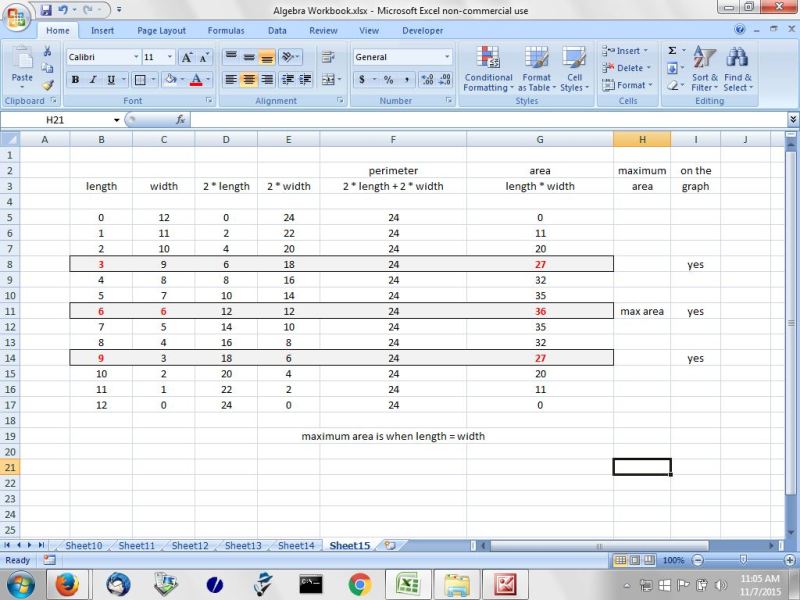
|
|
|
| |