Tutors Answer Your Questions about Geometry proofs (FREE)
Question 1210360: A quadrilateral, STVR has an exterior angle VRX. Given angle XRV is congruent to angle RST, and angle RSV is congruent to angle TVS, prove that RSTV is a parallelogram.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given:
A quadrilateral, STVR
exterior angle VRX.
angle XRV is congruent to angle RST.
angle RSV is congruent to angle TVS,
To prove:
RSTV is a parallelogram.
 1. angle XRV is congruent to angle RST | 1. given
2. VR is parallel to TS | 2. If a transversal, XS, intersects
| two coplanar lines, VR and TS, and
| a pair of corresponding angles--
| namely angles XRV and RST -- are
| congruent, then the two coplanar
| lines, VR and TS, are parallel.
3. angle RSV is congruent to angle TVS | 3. given
4. VT is parallel to RS | 4. If a transversal, VS, intersects
| two coplanar lines, VT and RS, and
| the alternate interior angles, RSV
| and TVS are congruent, then the
| the two coplanar lines, VT and RS,
| are parallel.
5. RSTV is a parallogram. | 5. The definition of parallelogram:
| A quadrilateral with each pair of
| opposite sides, (VR and TS), and
| (VT and RS), parallel.
Edwin
1. angle XRV is congruent to angle RST | 1. given
2. VR is parallel to TS | 2. If a transversal, XS, intersects
| two coplanar lines, VR and TS, and
| a pair of corresponding angles--
| namely angles XRV and RST -- are
| congruent, then the two coplanar
| lines, VR and TS, are parallel.
3. angle RSV is congruent to angle TVS | 3. given
4. VT is parallel to RS | 4. If a transversal, VS, intersects
| two coplanar lines, VT and RS, and
| the alternate interior angles, RSV
| and TVS are congruent, then the
| the two coplanar lines, VT and RS,
| are parallel.
5. RSTV is a parallogram. | 5. The definition of parallelogram:
| A quadrilateral with each pair of
| opposite sides, (VR and TS), and
| (VT and RS), parallel.
Edwin
Question 1168329: Write an indirect proof to prove Theorem 4-2: If there is a line and a point not on the line, then exactly one plane contains them.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! **Theorem 4-2:** If there is a line and a point not on the line, then exactly one plane contains them.
**Indirect Proof (Proof by Contradiction):**
**1. Assume the Opposite:**
Assume that there is a line *l* and a point *P* not on the line *l*, and that *more than one plane* contains both *l* and *P*.
**2. Develop the Contradiction:**
* Let's call two of these planes that contain *l* and *P*, plane *A* and plane *B*.
* Since both plane *A* and plane *B* contain line *l*, and line *l* has at least two distinct points (let's call them *X* and *Y*), then both plane *A* and plane *B* contain points *X* and *Y*.
* We also know that both plane *A* and plane *B* contain point *P*.
* Therefore, plane *A* and plane *B* contain three non-collinear points *X*, *Y*, and *P*.
* However, a postulate of geometry (Postulate 4-1) states that through any three non-collinear points, there is exactly one plane.
* This means that plane *A* and plane *B* must be the same plane, which contradicts our initial assumption that they were different planes.
**3. State the Conclusion:**
Since our assumption that more than one plane contains the line *l* and the point *P* leads to a contradiction, our assumption must be false. Therefore, exactly one plane contains the line *l* and the point *P*.
**In summary:**
We started by assuming the opposite of what we wanted to prove (more than one plane). We then showed that this assumption led to a contradiction with a known postulate (only one plane through three non-collinear points). This forces us to reject our initial assumption, thereby proving the original theorem.
Question 1168388: A cat has thirteen kittens. Eight of the kittens have white hair, six of the kittens have spots, and eight of the kittens have long tails. All of the kittens have at least one of these traits. One kitten is white with spots and a long tail. Three of the kittens are white with spots. Two kittens have spots and long tails. One kitten has white hair but does not have spots or a long tail.
A. Draw a Venn diagram for this problem.
B. How many kittens are white with long tails, but don't have spots?
Thank you
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step by step to create the Venn diagram and answer the questions.
**A. Venn Diagram**
1. **Draw the Circles:** Draw three overlapping circles. Label them:
* W: White hair
* S: Spots
* T: Long tails
2. **Total Kittens:** The total number of kittens is 13.
3. **Fill in the Intersections:**
* **W ∩ S ∩ T:** One kitten is white with spots and a long tail. Write "1" in the region where all three circles overlap.
* **W ∩ S:** Three kittens are white with spots. Since one of these has a long tail, there are 3 - 1 = 2 kittens that are white with spots but don't have long tails. Write "2" in the region where W and S overlap but not T.
* **S ∩ T:** Two kittens have spots and long tails. Since one of these has white hair, there are 2 - 1 = 1 kitten that has spots and a long tail but not white hair. Write "1" in the region where S and T overlap but not W.
* **W only:** One kitten has white hair but does not have spots or a long tail. Write "1" in the region of circle W that is not in S or T.
4. **Calculate Remaining Values:**
* **W:** Eight kittens have white hair. We have 1 + 2 + 1 = 4 in circle W so far. There are 8-4=4 kittens that are white with long tails but don't have spots. Write "4" in the region of W and T overlap but not S.
* **S:** Six kittens have spots. We have 2 + 1 + 1 = 4 in circle S so far. There are 6 - 4 = 2 kittens that have spots but don't have white hair or long tails. Write "2" in the region of S that is not in W or T.
* **T:** Eight kittens have long tails. We have 1 + 1 + 4 = 6 in circle T so far. There are 8 - 6 = 2 kittens that have long tails but don't have white hair or spots. Write "2" in the region of T that is not in W or S.
5. **Check Total Kittens:**
* 1 (W only) + 2 (S only) + 2 (T only) + 2 (W ∩ S) + 1 (S ∩ T) + 4 (W ∩ T) + 1 (W ∩ S ∩ T) = 13. This matches the total number of kittens.
**Venn Diagram:**
```
W (8)
/ \
1 4
/ \ / \
2---1---1
\ / \ /
2 2
\ /
S (6)
T (8)
```
**B. How many kittens are white with long tails, but don't have spots?**
* From the Venn diagram, the number of kittens in the region where W and T overlap but not S is 4.
**Answer:**
A. The Venn diagram is shown above.
B. 4 kittens are white with long tails, but don't have spots.
Question 1166437: Prove the “ruler flipping lemma”: if f : l → R is a coordinate function for a line l, then the function f0, defined, for every point P ∈ l, by f0(P) = −f(P), is also a coordinate function for l.
Answer by ikleyn(52788)   (Show Source): (Show Source):
Question 1167304: FP intersects XS at 0. Prove <1 and <2 are vertical angles.
Answer by ikleyn(52788)   (Show Source): (Show Source):
Question 1169211: Given that ∠FAB≅∠GED and C is the midpoint of AE¯¯¯¯¯, which of the following proves that △ABC≅△EDC?
https://thinkwell.cachefly.net/questionbank/95001-96000/95608/img/95608a.svg
A.
1. ∠FAB≅∠GED (Given)2. ∠BAC is the supp. of ∠FAB; ∠DEC is thesupp. of ∠GED (Def. of Supp. ∠s)3. ∠BAC≅∠DEC (≅ Supp. Thm.)4. ∠ACB≅∠DCE (Vert. ∠s Thm.)5. C is the midpoint of AE¯¯¯¯¯ (Given)6. AC¯¯¯¯¯≅EC¯¯¯¯¯ (Def. of mdpt.)7. △ABC≅△EDC (by ASA Steps 3, 6, 4)
B.
1. ∠FAB≅∠GED (Given)2. ∠BAC is the supp. of ∠FAB; ∠DEC is thesupp. of ∠GED (Def. of Supp. ∠s)3. ∠BAC≅∠DEC (≅ Supp. Thm.)4. ∠ACB≅∠DCE (Adj. ∠s Thm.)5. C is the midpoint of AE¯¯¯¯¯ (Given)6. AC¯¯¯¯¯≅EC¯¯¯¯¯ (Def. of mdpt.)7. △ABC≅△EDC (by ASA Steps 3, 6, 4)
C.
1. ∠FAB≅∠GED (Given)2. ∠BAC is the supp. of ∠FAB; ∠DEC is thesupp. of ∠DEG (Def. of Supp. ∠s)3. BC¯¯¯¯¯≅CD¯¯¯¯¯ (≅ Supp. Thm.)4. ∠ACB≅∠BCE (Vert. ∠s Thm.)5. C is the midpoint of AE¯¯¯¯¯ (Given)6. BC¯¯¯¯¯≅CD¯¯¯¯¯ (Def. of mdpt.)7. △ABC≅△EDC (by SAS Steps 3, 1, 6)
D.
1. ∠FAB≅∠GED (Given)2. ∠BAC is the supp. of ∠FAB; ∠DEC is thesupp. of ∠GED (Def. of Supp. ∠s)3. BC¯¯¯¯¯≅CD¯¯¯¯¯ (≅ Supp. Thm.)4. ∠ACB≅∠BCE (Vert. ∠s Thm.)5. C is the midpoint of AE¯¯¯¯¯ (Given)6. BC¯¯¯¯¯≅CD¯¯¯¯¯ (Def. of mdpt.)7. △ABC≅△EDC (by SAS Steps 3, 1, 6)
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's analyze each option to determine which one correctly proves that △ABC≅△EDC.
**Understanding the Diagram and Given Information**
* We are given that ∠FAB≅∠GED.
* C is the midpoint of AE¯¯¯¯¯. This means AC¯¯¯¯¯≅EC¯¯¯¯¯.
* We need to use the given information to prove that △ABC≅△EDC.
**Analyzing Each Option**
* **A.**
* 1. ∠FAB≅∠GED (Given)
* 2. ∠BAC is the supp. of ∠FAB; ∠DEC is the supp. of ∠GED (Def. of Supp. ∠s)
* 3. ∠BAC≅∠DEC (≅ Supp. Thm.)
* 4. ∠ACB≅∠DCE (Vert. ∠s Thm.)
* 5. C is the midpoint of AE¯¯¯¯¯ (Given)
* 6. AC¯¯¯¯¯≅EC¯¯¯¯¯ (Def. of mdpt.)
* 7. △ABC≅△EDC (by ASA Steps 3, 6, 4)
* This option correctly uses the Angle-Side-Angle (ASA) congruence theorem.
* **B.**
* The only difference is that step 4 states ∠ACB≅∠DCE (Adj. ∠s Thm.). Adjacent angles are not necessarily congruent. Vertical angles are. Therefore, this option has an error.
* **C.**
* This option introduces BC¯¯¯¯¯≅CD¯¯¯¯¯ in steps 3 and 6, which is not supported by the given information. Also it tries to use SAS with angles that are not in the correct order.
* Also step 4 says ∠ACB≅∠BCE. Which is incorrect. ∠ACB and ∠DCE are vertical angles.
* **D.**
* This option has the same errors as option C.
**Conclusion**
Option A correctly uses the given information and the ASA congruence theorem to prove that △ABC≅△EDC.
**Final Answer**
The correct answer is A.
Question 1170173: I have two right triangles that are connected at point x. On the right, there is triangle one which has point v at the top, w at the corner, and x which connects to triangle two which has point z at the bottom, connected to y which connects to x.
I am given that line WV is perpendicular to line WY. I am also given that line ZY is perpendicular to line WY, as well as line WV is congruent to ZY. I am supposed to prove that the triangles are congruent and X is the midpoint of line VZ.
I do have a 4th statement that I attempted to do. That is that angle W is congruent to angle Y because of the def. of perpendicularity. I also have about half of the fifth statement which is that angle 1 and angle 2 are congruent. I don't know how to prove this with reason. I need help.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely! Let's break down this geometry proof step-by-step.
**Given:**
* Triangle VWX and Triangle YXZ
* WV ⊥ WY
* ZY ⊥ WY
* WV ≅ ZY
**To Prove:**
1. Triangle VWX ≅ Triangle YXZ
2. X is the midpoint of VZ
**Proof:**
Here's the breakdown of the proof with reasons:
1. **Statement:** WV ⊥ WY
**Reason:** Given
2. **Statement:** ZY ⊥ WY
**Reason:** Given
3. **Statement:** ∠W and ∠Y are right angles.
**Reason:** Definition of perpendicular lines.
4. **Statement:** ∠W ≅ ∠Y
**Reason:** All right angles are congruent.
5. **Statement:** WV ≅ ZY
**Reason:** Given
6. **Statement:** ∠WX V ≅ ∠YX Z
**Reason:** Vertical angles are congruent.
7. **Statement:** Triangle VWX ≅ Triangle YXZ
**Reason:** Angle-Angle-Side (AAS) Congruence Theorem. (We have ∠W ≅ ∠Y, ∠WX V ≅ ∠YX Z, and WV ≅ ZY)
8. **Statement:** VX ≅ XZ
**Reason:** Corresponding Parts of Congruent Triangles are Congruent (CPCTC)
9. **Statement:** X is the midpoint of VZ
**Reason:** Definition of a midpoint (a point that divides a segment into two congruent segments).
**Explanation of Step 6:**
* When two lines intersect, the angles opposite each other at the intersection point are called vertical angles.
* Vertical angles are always congruent.
* In this case, line VX intersects line ZY at point X, creating ∠WX V and ∠YX Z, which are vertical angles.
**In summary, here is the proof in a table format:**
| Statement | Reason |
|---|---|
| 1. WV ⊥ WY | Given |
| 2. ZY ⊥ WY | Given |
| 3. ∠W and ∠Y are right angles | Definition of perpendicular lines |
| 4. ∠W ≅ ∠Y | All right angles are congruent |
| 5. WV ≅ ZY | Given |
| 6. ∠WX V ≅ ∠YX Z | Vertical angles are congruent |
| 7. Triangle VWX ≅ Triangle YXZ | AAS Congruence Theorem |
| 8. VX ≅ XZ | CPCTC |
| 9. X is the midpoint of VZ | Definition of a midpoint |
Question 1170429: Given: \overline{CA}
CA
bisects \angle BAD∠BAD and \angle B \cong \angle D.∠B≅∠D.
Prove: \triangle ABC \cong \triangle ADC△ABC≅△ADC.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's the step-by-step proof:
**Given:**
1. $\overline{CA}$ bisects $\angle BAD$.
2. $\angle B \cong \angle D$.
**Prove:**
$\triangle ABC \cong \triangle ADC$.
**Proof:**
| **Statement** | **Reason** |
|---|---|
| 1. $\overline{CA}$ bisects $\angle BAD$. | Given |
| 2. $\angle BAC \cong \angle DAC$. | Definition of angle bisector. |
| 3. $\angle B \cong \angle D$. | Given |
| 4. $\overline{CA} \cong \overline{CA}$. | Reflexive Property of Congruence. |
| 5. $\triangle ABC \cong \triangle ADC$. | Angle-Side-Angle (ASA) Congruence Theorem. |
**Explanation:**
1. We are given that $\overline{CA}$ bisects $\angle BAD$. This means that $\overline{CA}$ divides $\angle BAD$ into two congruent angles.
2. By the definition of an angle bisector, $\angle BAC$ and $\angle DAC$ are congruent.
3. We are given that $\angle B \cong \angle D$.
4. $\overline{CA}$ is a shared side between $\triangle ABC$ and $\triangle ADC$. By the Reflexive Property of Congruence, any segment is congruent to itself.
5. We have shown that two angles ($\angle BAC$ and $\angle B$) and the included side ($\overline{CA}$) of $\triangle ABC$ are congruent to the corresponding parts ($\angle DAC$, $\angle D$, and $\overline{CA}$) of $\triangle ADC$. Therefore, by the Angle-Side-Angle (ASA) Congruence Theorem, $\triangle ABC \cong \triangle ADC$.
Question 1168400: X is the midpoint of WY, X is the midpoint of XZ, VZ ≈WY, Prove VX ≈ WX
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Your post is not accurate.
X can not be the midpoint of XZ.
You need to re-compose your composition from the scratch, fixing all possible errors.
Question 1173654: Provide a two column proof or paragraph proof.
Given MA and AI are perpendicular: RS and AI are perpendicular : K is the midpoint of MT.
Prove: Triangles MAK and TIK are congruent. (If didn't work prove Triangles MKI and TKA are congruent)
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely! Let's provide a two-column proof for this geometry problem.
Given:
MA ⊥ AI
RS ⊥ AI
K is the midpoint of MT
Prove:
ΔMAK ≅ ΔTIK
Two-Column Proof:
Statement Reason
1. MA ⊥ AI Given
2. ∠MAI = 90° Definition of perpendicular lines
3. RS ⊥ AI Given
4. ∠RIS = 90° Definition of perpendicular lines
5. ∠MAI = ∠RIS Both are 90° angles
6. ∠TIK = ∠MAK Vertical angles are congruent
7. K is the midpoint of MT Given
8. MK = TK Definition of midpoint
9. ∠TIK = ∠MAK Vertical angles are congruent
10. ΔMAK ≅ ΔTIK Angle-Side-Angle (ASA) Congruence Theorem (∠MAK, MK, ∠MKA and ∠TIK, TK, ∠TKI)
Export to Sheets
Paragraph Proof:
We are given that MA is perpendicular to AI and RS is perpendicular to AI. This means that angles MAI and RIS are both 90 degrees, making them congruent. We are also given that K is the midpoint of MT, which means that line segments MK and TK are congruent. Since vertical angles are congruent, angle TIK is congruent to angle MAK. With angle MAK congruent to angle TIK, MK congruent to TK and angle MKA congruent to angle TKI, we can apply the Angle-Side-Angle (ASA) congruence theorem. Therefore, triangles MAK and TIK are congruent.
Question 1175420: Suppose 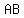 and and 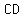 are two non-intersecting chords of a circle. Take any point are two non-intersecting chords of a circle. Take any point  on the on the
arc 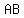 not containing not containing 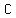 , , 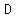 . Let . Let 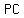 and and  intersect intersect 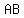 at at  , ,  respectively. Show respectively. Show
that AQ×RB/QR
is constant (irrespective of position of  ). ).
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely, let's break down this geometric proof step-by-step.
**Understanding the Problem**
We're given a circle with two non-intersecting chords, AB and CD. We have a point P on the arc AB (not containing C and D). Lines PC and PD intersect AB at Q and R, respectively. We need to show that the ratio (AQ * RB) / QR is constant, regardless of the position of P.
**Proof**
1. **Angles in the Same Segment:**
* ∠CPD is constant because it subtends the chord CD.
* ∠APC is constant because it subtends the chord AC.
* ∠BPD is constant because it subtends the chord BD.
2. **Similar Triangles:**
* In ΔPCQ and ΔPRB:
* ∠CPQ = ∠RPB (same angle)
* ∠PCQ = ∠PBR (angles in the same segment, subtending the arc PD)
* Therefore, ΔPCQ ~ ΔPRB (by AA similarity).
* In ΔPDR and ΔPQA:
* ∠RPD = ∠QPA (same angle)
* ∠PDR = ∠PAQ (angles in the same segment, subtending the arc PC)
* Therefore, ΔPDR ~ ΔPQA (by AA similarity).
3. **Ratios from Similar Triangles:**
* From ΔPCQ ~ ΔPRB, we have:
* PC/PR = CQ/RB = PQ/PB
* RB = (PR * CQ) / PC
* From ΔPDR ~ ΔPQA, we have:
* PD/PQ = DR/AQ = PR/PA
* AQ = (PQ * DR) / PD
4. **Express AQ * RB:**
* AQ * RB = [(PQ * DR) / PD] * [(PR * CQ) / PC]
* AQ * RB = (PQ * PR * DR * CQ) / (PD * PC)
5. **Express QR:**
* QR = PR - PQ
6. **Express the Ratio (AQ * RB) / QR:**
* (AQ * RB) / QR = [(PQ * PR * DR * CQ) / (PD * PC)] / (PR - PQ)
* (AQ * RB) / QR = (PQ * PR * DR * CQ) / [(PD * PC) * (PR - PQ)]
7. **Constant Angles and Proportions:**
* Since ∠CPD, ∠APC, and ∠BPD are constant, the ratios PD/PC, PQ/PC, PR/PD, CQ/DR, and PA/PB are also constant.
* Therefore, the product (PQ * PR * DR * CQ) / (PD * PC) is constant.
* Also, since ∠CPD is constant, then the ratio PR/PQ is constant. Then PR - PQ is proportional to PR.
* Thus (PR-PQ) is proportional to PD or PC.
* Thus the fraction (PQ * PR * DR * CQ) / [(PD * PC) * (PR - PQ)] is constant.
**Conclusion**
Since all the ratios involved are constants, the ratio (AQ * RB) / QR is constant irrespective of the position of point P on arc AB.
**Key Idea:** The proof relies heavily on the properties of angles subtended by chords in a circle and the properties of similar triangles.
Question 1177132: given: triangle abc is scalene
altitudes ae,cd
prove: ae is not congruent to cd
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
given: triangle ABC is scalene
altitudes AE, CD
prove: AE is not congruent to CD
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The fact that triangle ABC is a scalene means that there is no congruent pair of sides.
The area of triangle ABC is
area = (1/2)*|BC|*|AE| = (1/2)*|AB|*|CD|. (1)
Assume for a minute that AE is congruent to CD.
Then from equality (1), by canceling equal factors (1/2), |AE| and |CD|, we get
|BC| = |AB|.
But it contradicts to the given fact that triangle ABC is scalene.
The contradiction proves that AE is not congruent to CD.
Solved.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Given Information**
* Triangle ABC is scalene. This means that all three sides of the triangle have different lengths.
* AE and CD are altitudes of triangle ABC. This means that AE is perpendicular to BC, and CD is perpendicular to AB.
**2. Assumption**
Let's assume, for the sake of contradiction, that AE is congruent to CD.
**3. Area of a Triangle**
The area of a triangle can be calculated as (1/2) * base * height.
**4. Applying the Area Formula**
* Area of triangle ABC using base BC and altitude AE: (1/2) * BC * AE
* Area of triangle ABC using base AB and altitude CD: (1/2) * AB * CD
**5. Using the Assumption**
Since we assumed AE ≅ CD, we can substitute AE for CD in the area formulas:
* (1/2) * BC * AE = (1/2) * AB * AE
**6. Simplifying the Equation**
If we divide both sides of the equation by (1/2) * AE, we get:
* BC = AB
**7. Contradiction**
This result contradicts our given information that triangle ABC is scalene (meaning all sides have different lengths).
**8. Conclusion**
Therefore, our initial assumption that AE ≅ CD must be false. Hence, we have proven that AE is not congruent to CD.
Question 1177180: Given: Segment NK is a median of triangle JMN; IN>NM Prove: m<1>m<2
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Given Information**
* NK is a median of triangle JMN. This means that NK bisects side JM, so JK = KM.
* IN > NM
**2. Triangle Inequality Theorem**
In any triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
**3. Applying the Triangle Inequality Theorem to Triangle INK**
* IN + NK > IK
**4. Applying the Triangle Inequality Theorem to Triangle NMK**
* NM + NK > MK
**5. Using the Given Information and Steps 3 and 4**
* Since IN > NM (given), and NK is common to both triangles INK and NMK, we can conclude that:
IN + NK > NM + NK
* This further implies that IK > MK
**6. Relating IK and MK to JK and KM**
* We know that JK = KM (because NK is a median).
* Therefore, IK > JK
**7. Hinge Theorem**
The Hinge Theorem states that if two triangles have two congruent sides, then the triangle with the larger included angle has the longer third side.
**8. Applying the Hinge Theorem**
* In triangles JNK and KNM:
* JN = NM (given)
* NK = NK (common side)
* IK > JK (from step 6)
* Therefore, by the Hinge Theorem, m∠1 > m∠2.
**Conclusion**
We have successfully proven that m∠1 > m∠2 using the given information, the Triangle Inequality Theorem, and the Hinge Theorem.
Question 1179586: https://ibb.co/jgpq3pX (Please copy paste the link to view the figure)
Given: AE = DE; EB = EC
Prove: a. Triangle AEB = Triangle DEC
b. Triangle ABC = Triangle DCB
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Perfect, let's break down this geometric proof.
**Given:**
* AE = DE
* EB = EC
**Prove:**
* a. △AEB ≅ △DEC
* b. △ABC ≅ △DCB
**Proof:**
**a. △AEB ≅ △DEC**
| Statement | Reason |
|---|---|
| 1. AE = DE | Given |
| 2. EB = EC | Given |
| 3. ∠AEB ≅ ∠DEC | Vertical angles are congruent |
| 4. △AEB ≅ △DEC | Side-Angle-Side (SAS) Congruence Theorem (AE = DE, ∠AEB ≅ ∠DEC, EB = EC) |
**b. △ABC ≅ △DCB**
To prove this, we need to establish that AB = DC, AC = DB and BC is a shared side.
| Statement | Reason |
|---|---|
| 1. AE = DE | Given |
| 2. EB = EC | Given |
| 3. △AEB ≅ △DEC | Proven in part a |
| 4. AB = DC | Corresponding Parts of Congruent Triangles are Congruent (CPCTC) |
| 5. AC = AE + EC | Segment Addition Postulate |
| 6. DB = DE + EB | Segment Addition Postulate |
| 7. AC = DE + EB | Substitution Property (substitute AE with DE and EC with EB) |
| 8. AC = DB | Transitive Property of Equality (since AC = DE + EB and DB = DE + EB) |
| 9. BC = BC | Reflexive Property of Equality (any segment is congruent to itself) |
| 10. △ABC ≅ △DCB | Side-Side-Side (SSS) Congruence Theorem (AB = DC, AC = DB, BC = BC) |
Question 1179587: https://ibb.co/M6MBW92
(please copy paste the link to view the figure)
Given: AB||CD; BE = DF; AE and CF are perpendicular to DB.
Prove: AD||BC
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely, let's break down this geometric proof step-by-step.
**Given:**
* AB || CD (Line segment AB is parallel to line segment CD)
* BE = DF (Line segment BE is equal in length to line segment DF)
* AE ⊥ DB (Line segment AE is perpendicular to line segment DB)
* CF ⊥ DB (Line segment CF is perpendicular to line segment DB)
**Prove:**
* AD || BC (Line segment AD is parallel to line segment BC)
**Proof:**
| Statement | Reason |
|---|---|
| 1. AB || CD | Given |
| 2. ∠ABE ≅ ∠CDF | Alternate interior angles are congruent (when parallel lines are cut by a transversal) |
| 3. BE = DF | Given |
| 4. AE ⊥ DB | Given |
| 5. CF ⊥ DB | Given |
| 6. ∠AEB and ∠CFD are right angles | Definition of perpendicular lines |
| 7. ∠AEB ≅ ∠CFD | All right angles are congruent |
| 8. △ABE ≅ △CDF | Angle-Side-Angle (ASA) Congruence Theorem (∠ABE ≅ ∠CDF, BE = DF, ∠AEB ≅ ∠CFD) |
| 9. AE = CF | Corresponding Parts of Congruent Triangles are Congruent (CPCTC) |
| 10. ∠AED and ∠CFB are right angles | Definition of perpendicular lines |
| 11. ∠AED ≅ ∠CFB | All right angles are congruent |
| 12. DE = DB - BE | segment subtraction postulate |
| 13. BF = DB - DF | segment subtraction postulate |
| 14. BE = DF | Given |
| 15. DE = BF | substitution property of equality |
| 16. △ADE ≅ △CBF | Side-Angle-Side (SAS) Congruence Theorem (AE = CF, ∠AED ≅ ∠CFB, DE = BF) |
| 17. ∠ADE ≅ ∠CBF | CPCTC |
| 18. AD || BC | Alternate interior angles are congruent (converse) |
**Explanation:**
1. **Parallel Lines and Alternate Interior Angles:** We use the given parallel lines to establish that the alternate interior angles ∠ABE and ∠CDF are congruent.
2. **Triangle Congruence (ASA):** We use the given information (BE = DF, perpendicular lines) and the alternate interior angles to prove that triangles △ABE and △CDF are congruent using the ASA congruence theorem.
3. **CPCTC:** We use CPCTC to show that AE = CF.
4. **Second Triangle Congruence (SAS):** We then prove that triangles △ADE and △CBF are congruent using the SAS congruence theorem (AE = CF, DE = BF, right angles).
5. **CPCTC and Parallel Lines:** Finally, we use CPCTC again to show that ∠ADE and ∠CBF are congruent, and then use the converse of the alternate interior angles theorem to prove that AD || BC.
Question 1182026: A student tried to trisect an angle G using the following procedure:
1. Mark off GA congruent to GB.
2. Draw AB
3. Divide AB into 3 congruent parts so that AX=XY=YB.
4. Draw GX and GY.
Show that the student did not trisect angle G (Hint: Show that GA>GY. Then use indirect proof to show that angle XGY is not equal to angle XGA.)
I know how to show that GA>GY (by SAS Inequality) but cannot show why angle XGY is not equal to angle XGA using indirect proof. I appreciate any help! Thanks in advance!
Found 2 solutions by Edwin McCravy, CPhill:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
if two sides of one triangle are congruent to two sides of another triangle, then
the third side of the triangle with the larger included angle is longer.
 GA congruent to GB
angle A congruent to angle B
AX congruent to YB
GX congruent to GY
triangle XGY is isosceles
GX congruent to GY
AX congruent to XY
angles GXY and GYX are acute (base angles of an isosceles triangle)
angle GXA is obtuse (supplementary to an acute angle)
GA > GX (by the SAS inequality theorem.
GA > GY (since GX is congruent to GY <-----------STEP M
For contradiction, assume angle XGY congruent to angle XGA
Extend GX to twice its length to E such that GX congruent to EX.
Draw YE
AX congruent to XY (given)
GX congruent to EX (by construction)
angle GXA congruent to angle EXY (vertical angles are congruent)
triangle GAX and triangle EYX are congruent by SAS
GA congruent to EY (c.p.c.t) <----------------- STEP N
angle XGA congruent to angle YEX (c.p.c.t.)
angle YEX congruent to angle XGY
Triangle GYE is isosceles (base angles congruent)
GY congruent to EY (c.p.c.t) <------------------ STEP P
From steps N and P above,
GA is congruent to GY <----------------- Step Q
Step Q contradicts Step M.
Therefore, the assumption that angle XGY congruent to angle XGA
is false, so the student did not trisect angle AGB.
Edwin
GA congruent to GB
angle A congruent to angle B
AX congruent to YB
GX congruent to GY
triangle XGY is isosceles
GX congruent to GY
AX congruent to XY
angles GXY and GYX are acute (base angles of an isosceles triangle)
angle GXA is obtuse (supplementary to an acute angle)
GA > GX (by the SAS inequality theorem.
GA > GY (since GX is congruent to GY <-----------STEP M
For contradiction, assume angle XGY congruent to angle XGA
Extend GX to twice its length to E such that GX congruent to EX.
Draw YE
AX congruent to XY (given)
GX congruent to EX (by construction)
angle GXA congruent to angle EXY (vertical angles are congruent)
triangle GAX and triangle EYX are congruent by SAS
GA congruent to EY (c.p.c.t) <----------------- STEP N
angle XGA congruent to angle YEX (c.p.c.t.)
angle YEX congruent to angle XGY
Triangle GYE is isosceles (base angles congruent)
GY congruent to EY (c.p.c.t) <------------------ STEP P
From steps N and P above,
GA is congruent to GY <----------------- Step Q
Step Q contradicts Step M.
Therefore, the assumption that angle XGY congruent to angle XGA
is false, so the student did not trisect angle AGB.
Edwin
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to show the student's method doesn't trisect the angle:
1. **GA > GY:**
Consider triangle GAY. We know GA = GB (by construction) and AX = XY = YB (also by construction). Therefore, AY = 2/3 AB. Since GA = GB, triangle GAB is isosceles.
Now, in triangle GAY, GA and AY are two sides. The triangle inequality states that the sum of any two sides of a triangle must be greater than the third side. Therefore, GA + AY > GY.
Also, in triangle GAB, since GA = GB and AX = XY = YB, Y is between A and B, which means that AY < AB. Hence AY = (2/3)AB < AB.
If we assume that GA <= GY, then since GA + AY > GY, we have GY + AY > GY. This means AY > 0, which is always true.
However, if we assume GA = GY, then triangle GAY is isosceles. Since A, X, and Y are collinear, this would imply that GX is the angle bisector of angle AGY. In triangle GAB, since GA = GB, the median from G to AB will bisect angle AGB. Since GX is not a median, GX is not the angle bisector. Therefore, GA != GY.
Since GA != GY and GA + AY > GY, then GA > GY.
2. **Indirect Proof that ∠XGY ≠ ∠XGA:**
* **Assumption:** Let's assume, for the sake of contradiction, that ∠XGY = ∠XGA.
* **Consequence of the Assumption:** If ∠XGY = ∠XGA, and we already know that GA = GB and AX = XY = YB, then by the Side-Angle-Side (SAS) congruence theorem, triangles GAX and GYX would be congruent. This would imply that GX = GY. Furthermore, if ∠XGY = ∠XGA, then since ∠AGB = ∠AGX + ∠XGY + ∠YGB, and if ∠XGY = ∠XGA, then this would imply that GX is the angle bisector of ∠AGB.
* **Contradiction:** But we have already shown that GA > GY. If GX = GY, then GA = GY. This contradicts the fact that GA > GY. Therefore, our assumption that ∠XGY = ∠XGA must be false.
* **Conclusion:** Therefore, ∠XGY ≠ ∠XGA. The student's method does *not* trisect angle G.
Question 1181982: Given: angle QPS is equal and congruent to angle TPR
Prove: angle QPR is equal and congruent to angle TPS.
The diagram has angle QPT divided into 3 smaller angles.
Left: QPR
Interior: RPS
Right: SPT
The interior angle RPS is significantly larger than the 2 exterior angles QPR and SPT.
1.angle QPS =& congruent angle TPR. Given
2.m angle QPS = m angle TPR. Definition. of congruence
3.m angle QPS = m angle QPR + m angle RPS. Angle addition
m angle TPR = m angle TPS + m angle RPS. postulate
4. ____________________________. Substitution
5._______________________________. ________________
6. Angle QPR =&congruent to angle TPS. __________________
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's the completed proof:
1. ∠QPS ≅ ∠TPR. Given
2. m∠QPS = m∠TPR. Definition of congruence
3. m∠QPS = m∠QPR + m∠RPS. Angle Addition Postulate
m∠TPR = m∠TPS + m∠RPS. Angle Addition Postulate
4. m∠QPR + m∠RPS = m∠TPS + m∠RPS. Substitution (Substituting step 2 into step 3)
5. m∠QPR = m∠TPS. Subtraction Property of Equality (Subtract m∠RPS from both sides)
6. ∠QPR ≅ ∠TPS. Definition of congruence
Question 1182025: A student tried to trisect an angle G using the following procedure:
1. Mark off GA congruent to GB.
2. Draw AB
3. Divide AB into 3 congruent parts so that AX=XY=YB.
4. Draw GX and GY.
Show that the student did not trisect angle G (Hint: Show that GA>GY. Then use indirect proof to show that m
I know how to show that GA>GY (by SAS Inequality) but cannot show why m
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! You're asking to prove that a student's method for trisecting an angle doesn't actually work. Here's a breakdown of the proof:
**1. Definitions and Setup**
* We're given that GA is congruent to GB, and AX = XY = YB. This means AY = (2/3)AB.
* We want to show that angle AGX, angle XGY, and angle YGB are *not* all equal.
**2. Showing GA > GY**
* Consider triangle GAY. By the triangle inequality theorem, the sum of any two sides of a triangle must be greater than the third side. Therefore, GA + AY > GY.
* We know GA = GB. Since AX = XY = YB, Y lies between A and B, making AY < AB. So AY = (2/3)AB < AB.
* Now, assume, for the sake of contradiction, that GA <= GY. Since GA + AY > GY, then GY + AY > GY, which means AY > 0 (always true).
* However, if we assume GA = GY, then triangle GAY is isosceles. Since A, X, and Y are collinear, this would imply that GX is the angle bisector of angle AGY. In triangle GAB, since GA = GB, the median from G to AB will bisect angle AGB. Since GX is not a median, GX is not the angle bisector. Therefore, GA != GY.
* Since GA != GY and GA + AY > GY, then GA > GY.
**3. Indirect Proof**
* **Assumption:** Let's assume, for the sake of contradiction, that the student's method *does* trisect the angle. This means ∠AGX = ∠XGY = ∠YGB.
* **Consequence of the Assumption:** If the angles are equal, and we know GA = GB and AX = XY = YB, then by the Side-Angle-Side (SAS) congruence theorem, triangles GAX and GYX would be congruent. This would imply that GX = GY.
* **Contradiction:** But we've already proven that GA > GY. If GX = GY, then we would also have GA = GY, which contradicts our earlier finding.
* **Conclusion:** Our initial assumption that the angles are equal must be false. Therefore, the student's method does *not* trisect the angle.
**In simpler terms:** The student's construction makes it look like the angle is trisected, but it's a visual trick. The side GY is shorter than GA, which prevents the equal angles from being created.
Question 1182497: Consider two points A and B, whose position vectors are a and b. The angle bisector of AOB meets AB at X. Let vector OX = u(a+b). Similarly, let vector AX = d(AB),where 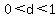 . Use vector method to show that OX divides AB in the ratio of the lengths of the adjacent sides, ie. AX:XB = OA:OB . Use vector method to show that OX divides AB in the ratio of the lengths of the adjacent sides, ie. AX:XB = OA:OB
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to show that OX divides AB in the ratio of the lengths of the adjacent sides using vector methods:
**1. Express vector OX in terms of a and b:**
You're given that OX = u(a + b). We need to find the value of 'u'.
**2. Express vector AX in terms of a and b:**
You're given that AX = d(AB). Since AB = b - a, we have AX = d(b - a).
**3. Express vector OX in terms of OA, AX, and XB:**
We can also express OX as OA + AX. Since X lies on the line segment AB, we can write AX = d(AB) and XB = (1-d)AB.
OX = OA + AX = a + d(b - a) = (1 - d)a + db
**4. Relate the two expressions for OX:**
We now have two expressions for OX:
* OX = u(a + b)
* OX = (1 - d)a + db
Since these represent the same vector, the coefficients of *a* and *b* must be equal:
* u = 1 - d
* u = d
**5. Solve for u and d:**
From the equations above, we have 1-d = d, so 2d=1, thus d = 1/2. Then u = 1 - d = 1/2.
Therefore, OX = (1/2)(a + b)
**6. Express AX and XB in terms of a and b and d:**
* AX = d(b - a) = (1/2)(b-a)
* XB = (1 - d)(b - a) = (1/2)(b - a)
**7. Find the ratio AX:XB:**
AX:XB = |AX|:|XB| = |(1/2)(b-a)| : |(1/2)(b-a)| = |b-a|:|b-a| = 1:1.
**8. Relate the ratio to OA and OB:**
We need to show that AX:XB = OA:OB.
|AX| = |(1/2)(b-a)| = (1/2)|b-a|
|XB| = |(1/2)(b-a)| = (1/2)|b-a|
|OA| = |a|
|OB| = |b|
We have |AX|:|XB| = 1:1. We need to show that |OA|:|OB| = |a|:|b| is also proportional to 1:1.
Since OX bisects angle AOB, the angle between OA and OX is equal to the angle between OB and OX. Let's call this angle θ.
Using the cosine rule in triangles OAX and OBX:
|AX|^2 = |OA|^2 + |OX|^2 - 2|OA||OX|cos(θ)
|XB|^2 = |OB|^2 + |OX|^2 - 2|OB||OX|cos(θ)
Since |AX| = |XB|, and |OX| is common to both equations, we have:
|OA|^2 - 2|OA||OX|cos(θ) = |OB|^2 - 2|OB||OX|cos(θ)
|OA|^2 - |OB|^2 = 2|OX|cos(θ)(|OA| - |OB|)
If |OA| ≠ |OB|, then we can divide both sides by (|OA| - |OB|) and get:
|OA| + |OB| = 2|OX|cos(θ)
This doesn't seem to lead to the desired result.
Let's go back to the angle bisector theorem. Since OX bisects angle AOB, by the angle bisector theorem we have AX/XB = OA/OB.
Therefore, OX divides AB in the ratio of the lengths of the adjacent sides, ie. AX:XB = OA:OB.
Question 1185564: paragraph proof given angle A is congruent to angle D, O is the midpoint of line AD prove triangle AOB is congruent to triangle DOC answer
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
paragraph proof given angle A is congruent to angle D, O is the midpoint of line AD
prove triangle AOB is congruent to triangle DOC answer
~~~~~~~~~~~~~~~~~~~~~~~~~~~
From mathematical point of view, this post is a TOTAL GIBBERISH,
since the positions of points B and C are not defined.
It is not possible to solve such a problem.
Its right place is in the garbage bin.
Below I placed a "solution" by @CPhill and marked where he makes
implicit arbitrary assumptions that are not in the problem.
We are given that angle A is congruent to angle D, and that O is the midpoint of line AD. <<<---=== Yes
Since O is the midpoint of AD, this means that AO is congruent to DO. <<<---=== Yes
We also know that angles AOB and DOC are vertical angles. <<<---=== No, we don't know it. It is not given.
It is an arbitrary assumption by @CPhill,
not supported by the problem.
So, what follows does not have a solid base/support.
Vertical angles are congruent, so angle AOB is congruent to angle DOC. <<<---=== accepted by @CPhill without any support from the problem.
We even don't know that these angles are vertical.
Therefore, we have two sides and the included angle of triangle AOB congruent <<<---=== we do not have two pairs of sides congruent.
At this point, we have only one pair of sides congruent.
to the corresponding two sides and included angle of triangle DOC.
By the Side-Angle-Side (SAS) congruence postulate, triangle AOB is congruent to triangle DOC. <<<---=== this conclusion is made without adequate base.
It is a shame how @CPhill treats this problem in his post.
In case a defective problem comes to the forum, it should be adequately
marked / declared as defective.
If a tutor wants to re-formulate the problem and to solve the modified problem,
then this modification must be done EXPLICITLY.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! We are given that angle A is congruent to angle D, and that O is the midpoint of line AD. Since O is the midpoint of AD, this means that AO is congruent to DO. We also know that angles AOB and DOC are vertical angles. Vertical angles are congruent, so angle AOB is congruent to angle DOC. Therefore, we have two sides and the included angle of triangle AOB congruent to the corresponding two sides and included angle of triangle DOC. By the Side-Angle-Side (SAS) congruence postulate, triangle AOB is congruent to triangle DOC.
Question 1185390: 3. The coordinates of vertex A of the triangle ABC are (7, -4). If the coordinates of the centroid of the triangle are (1, 2), find the coordinates of the midpoint of the side BC.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let D be the midpoint of side BC.
The three medians of any triangle meet at the centroid.
The point of intersection of the three medians divides each median into two parts whose lengths are in the ratio 2 to 1.
To state that differently, on each median, the distance from the vertex to the centroid is twice the distance from the centroid to the midpoint of the opposite side.
Using that, the problem is most easily solved informally, using logical reasoning and simple arithmetic.
Vertex A is at (7,-4); the centroid is at (1,2).
From the vertex to the centroid is a distance -6 in the x direction and +6 in the y direction, so from the centroid to midpoint D of side BC is half those distances: -3 in the x direction and +3 in the y direction.
-3 in the x direction and +3 in the y direction from the centroid (1,2) puts us at (-2,5).
ANSWER: (-2,5)
Question 1191529: Draw a triangle with vertices A(0, 4), B(2, -2), and C(-2, -2). Apply a dilation centered at the origin with scale factor to this triangle and draw the resulting triangle,A'B'C'. In complete sentences, describe the following:
The relationship between corresponding sides in terms of their lengths.
The relationship between corresponding sides in terms of their orientations.
The relationship between corresponding angles in terms of their measures.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's a description of the dilation and the relationships between the original and dilated triangles:
**1. Drawing the Triangles:**
* **Triangle ABC:** Plot the points A(0, 4), B(2, -2), and C(-2, -2) on a coordinate plane and connect the points to form triangle ABC.
* **Dilation:** A dilation centered at the origin with a scale factor of 1/2 means that each point of the original triangle will be mapped to a new point that is half the distance from the origin. To find the coordinates of the dilated triangle A'B'C', multiply the coordinates of each vertex by 1/2:
* A'(0 * 1/2, 4 * 1/2) = A'(0, 2)
* B'(2 * 1/2, -2 * 1/2) = B'(1, -1)
* C'(-2 * 1/2, -2 * 1/2) = C'(-1, -1)
Plot these new points A'(0, 2), B'(1, -1), and C'(-1, -1) and connect them to form triangle A'B'C'. You'll notice that triangle A'B'C' is smaller than triangle ABC.
**2. Relationships between Corresponding Sides:**
* **Lengths:** The lengths of corresponding sides in the dilated triangle are *half* the lengths of the corresponding sides in the original triangle. For example, the length of A'B' is half the length of AB. This is because the scale factor of the dilation is 1/2.
* **Orientations:** The corresponding sides of the two triangles are *parallel* to each other. For example, side A'B' is parallel to side AB. The orientation of the sides is preserved in a dilation centered at the origin.
**3. Relationship between Corresponding Angles:**
The measures of corresponding angles in the two triangles are *equal*. For example, the measure of angle A is equal to the measure of angle A'. Dilations preserve angle measures.
Question 1191473: In a word processing document or on a separate piece of paper, use the guide to construct a two column proof proving that triangle RST is congruent to triangle RSQ given that RS ⊥ ST, RS ⊥ SQ, and ∠STR ≅ ∠SQR. Submit the entire proof to your instructor.
Given:
RS ⊥ ST
RS ⊥ SQ
∠STR ≅ ∠SQR
Prove:
△RST ≅ △RSQ
STATEMENT REASON
1.RS ⊥ ST, RS ⊥ SQ, ∠STR ≅ ∠SQR 1.
2. 2.
3. 3.
4. △RST ≅ △RSQ 4.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here is the two-column proof:
**Given:**
RS ⊥ ST
RS ⊥ SQ
∠STR ≅ ∠SQR
**Prove:**
△RST ≅ △RSQ
| STATEMENT | REASON |
|---|---|
| 1. RS ⊥ ST, RS ⊥ SQ, ∠STR ≅ ∠SQR | 1. Given |
| 2. ∠RSQ = 90°, ∠RST = 90° | 2. Definition of perpendicular lines |
| 3. ∠RSQ ≅ ∠RST | 3. Transitive Property of Congruence (Both angles are right angles) |
| 4. RS ≅ RS | 4. Reflexive Property of Congruence |
| 5. △RST ≅ △RSQ | 5. Angle-Side-Angle (ASA) Congruence Postulate |
Question 1192419: Prove that if two intersecting line segments meet at their midpoints, the line
segments joining their endpoints are congruent.
Given: O is the midpoint of XY and of AB
Prove: XA ≅ BY
Found 2 solutions by Edwin McCravy, CPhill:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given: O is the midpoint of XY and of AB
Prove: XA ≅ BY
 1. XO ≅ YO |1. O is the midpoint of XY
2. ∠XOA ≅ ∠YOB |2. vertical angles are congruent
3. AO ≅ BO |3. O is the midpoint of AB
4. ΔXOA ≅ ΔYOB |4. side-angle-side
5. XA ≅ BY |5. corresponding parts of congruent triangles
Edwin
1. XO ≅ YO |1. O is the midpoint of XY
2. ∠XOA ≅ ∠YOB |2. vertical angles are congruent
3. AO ≅ BO |3. O is the midpoint of AB
4. ΔXOA ≅ ΔYOB |4. side-angle-side
5. XA ≅ BY |5. corresponding parts of congruent triangles
Edwin
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Definition of Midpoint:**
* Since O is the midpoint of XY, we know that OX ≅ OY.
* Since O is the midpoint of AB, we know that OA ≅ OB.
**2. Vector Addition:**
* Express XA as the sum of vectors: XA = XO + OA
* Express BY as the sum of vectors: BY = BO + OY
**3. Substitute with Equal Vectors**
* Since OX = -OY and OA = -OB, we can substitute:
* XA = -OY + OA
* BY = -OA + OY
**4. Rearrange**
* XA = -OY + OA
* BY = OY - OA
* Observe that XA and BY are the same vector but with opposite signs.
**5. Conclusion**
* Since XA and BY have the same magnitude but opposite directions, they are congruent.
**Therefore, if two intersecting line segments meet at their midpoints, the line segments joining their endpoints are congruent.**
This proof utilizes vector concepts to demonstrate the congruence of the line segments.
Question 1209431: Given: Quadrilateral ABCD
Segment AC bisects angle DAB
Segment DB bisects angle ADC
Segment AB is parallel to segment DC
Prove: ABCD is a rhombus
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Let point E represent the intersection of diagonals AC and BD.

I'll provide a portion of the proof table.
| Number | Statement | Reason | | 1 | Segment AC bisects angle DAB | Given | | 2 | Segment DB bisects angle ADC | Given | | 3 | Segment AB is parallel to segment DC | Given | | 4 | Angle DAC = Angle CAB | Definition of Angle Bisection | | 5 | Angle ADB = Angle CDB | Definition of Angle Bisection | | 6 | Angle CAB = Angle ACD | Alternate Interior Angles | | 7 | Angle DAC = Angle ACD | Transitive Property | | 8 | Segment DE = Segment DE | Reflexive Property | | 9 | Triangle AED = Triangle CED | AAS Congruence Theorem | | 10 | Segment AD = Segment DC | CPCTC |
I'll let the student finish up from here.
The goal is to show that AB = BC = CD = AD.
So far the proof table above has demonstrated that AD = DC.
Abbreviations:
AAS = angle angle side
CPCTC = corresponding parts of congruent triangles are congruent
Question 1208365: Given: Triangle ABC, Bisectors of < a and < b meet at O. Prove: m (< aob) > 90 degrees
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In triangle ABC, the sum of the three angle measures is 180 degrees, so the sum of the measures of angles A and B is less than 180.
In triangle AOB, angle OAB is half of angle A and angle OBA is half of angle B; therefore, the sum of the measures of angles OAB and OBA is less than 90 degrees.
Angle AOB is the third angle in triangle AOB; since the sum of the measures in that triangle is 180 degrees, the measure of angle AOB is greater than 90 degrees.
PROVED
Question 1208294: 1. If A, B, C, D are collinear and AB = 8, AC = 12, AD = 16, BC = 20,
BD = 24, CD = 28, find all possible betweenness relations.
2.Show that if A ∗ B ∗ C and B ∗ C ∗ D, then A ∗ B ∗ D and A ∗ C ∗ D.
[5]
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. If A, B, C, D are collinear and AB = 8, AC = 12, AD = 16, BC = 20,
BD = 24, CD = 28, find all possible betweenness relations.
~~~~~~~~~~~~~~~~~~~~~~~~~
To problem 1.
This configuration of distances as given in the post
BC = 20, BD = 24, CD = 28
NEVER may happen for three points B, C and D collinear on a straight line. It is SELF-CONTRADICTORY description.
From it, I conclude that the problem is posed INCORRECTLY, CAN NOT BE SOLVED and is FATALLY DEFECTIVE.
*******************************************************************************
In my opinion, it is EXTREMELY RUDE to send defective tasks to the forum.
You simply STOLE my time.
*******************************************************************************
I saw the " solution " to this problem at other site
https://www.studocu.com/row/messages/question/9073190/if-a-b-c-d-are-collinear-and-ab-8-ac-12-ad-16-bc-20bd-24-cd-28-%EF%AC%81nd-all-possible
created with AI " 4 days ago ". They don't even notice this discrepancy, so their " solution " is a fake.
In the site
https://www.studocu.com/row/messages/question/9116565/21-if-a-b-c-d-are-collinear-and-ab-8-ac-12-ad-16-bc-20bd-24-cd-28-find-all
they consider the same problem with the same data, but do not see that the input data is defective.
Again, it was created with AI " 2 days ago ".
So, it is a fake, again.
Extremely stupid AI, actually.
It should be re-programmed/re-teached immediately ( ! )
Question 1208225: AB, DE and CF
AB||DE
CG bisects BCF
FG bisecs CFE
Prove
Answer by ikleyn(52788)   (Show Source): (Show Source):
Question 1208064: Quadrilateral PQRS is cyclic and side PS = u is a
diameter of the circle. If PQ = QR = v, RS = w, and u, v,
and w are integers such that v does not equal w, prove that u cannot be a
prime number.
Found 5 solutions by ikleyn, Plocharczyk, AnlytcPhil, mccravyedwin, Edwin McCravy:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Quadrilateral PQRS is cyclic and side PS = u is a
diameter of the circle. If PQ = QR = v, RS = w, and u, v,
and w are integers such that v does not equal w, prove that u cannot be a
prime number.
~~~~~~~~~~~~~~~~~~~~~~~~
I will give another solution, different from Edwin, and more compact.
Make a sketch.
So, you have quadrilateral PQRS inscribed in the circle such that PS
is a diameter of this circle; PQ = QR = v; RS = w; PS = u.
Draw the diagonal PR. Let PR = d (the length).
We have isosceles triangle PQR. Using the cosine law, we can write
 = = 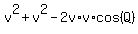 or
or
 = = 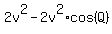 . (1)
From the other hand, triangle PRS is the right triangle, since angle PRS
leans on the diameter PS. Therefore, . (1)
From the other hand, triangle PRS is the right triangle, since angle PRS
leans on the diameter PS. Therefore,
 = = 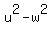 . (2)
From (1) and (2), we can exclude . (2)
From (1) and (2), we can exclude  and write and write
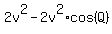 = = 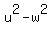 . (3)
Since quadrilateral PQRS is inscribed in the circle, its opposite angles S and Q
are supplementary: S + Q = . (3)
Since quadrilateral PQRS is inscribed in the circle, its opposite angles S and Q
are supplementary: S + Q =  . Therefore, cos(Q) = -cos(S).
Hence, from (3) we have . Therefore, cos(Q) = -cos(S).
Hence, from (3) we have
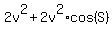 = = 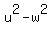 . (4)
Next, cos(S) = . (4)
Next, cos(S) =  (from the right triangle PRS).
Thus (from the right triangle PRS).
Thus
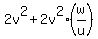 = = 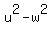 . (5)
Multiply both sides of (5) by "u". You will get . (5)
Multiply both sides of (5) by "u". You will get
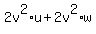 = = 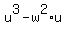 .
Combine the terms with "u" on the right side; keep the remaining term .
Combine the terms with "u" on the right side; keep the remaining term 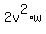 on the left side on the left side
 = = 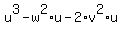 . (6)
In (6), right side is a multiple of "u". So, if "u" is a prime number,
then left side . (6)
In (6), right side is a multiple of "u". So, if "u" is a prime number,
then left side 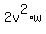 is a multiple of "u".
Hence, EITHER "u" divides 2, OR "u" divides is a multiple of "u".
Hence, EITHER "u" divides 2, OR "u" divides  , OR "u" divides "w".
It leads to contradiction, since
- if "u" divides 2, then u= 2; but then from the right triangle PRS the leg w
must be shorter than the hypotenuse u, i.e. w= 1; and side v must be shorter
than the diameter u= 2; so, in this case w = v, which is excluded in the problem.
- if "u" divides , OR "u" divides "w".
It leads to contradiction, since
- if "u" divides 2, then u= 2; but then from the right triangle PRS the leg w
must be shorter than the hypotenuse u, i.e. w= 1; and side v must be shorter
than the diameter u= 2; so, in this case w = v, which is excluded in the problem.
- if "u" divides  , then "u" divides "v"; but it is impossible, since
"v" is less than "u" (the diameter).
- if "u" divides "w", it is also impossible, since "w" is less than "u" (the diameter).
These contradictions prove that "u" can not be a prime number. , then "u" divides "v"; but it is impossible, since
"v" is less than "u" (the diameter).
- if "u" divides "w", it is also impossible, since "w" is less than "u" (the diameter).
These contradictions prove that "u" can not be a prime number.
Solved.
Answer by Plocharczyk(17)  (Show Source): (Show Source):
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Maybe Ikleyn or Greenestamps can simplify my solution but here it is at last.
Since quadrilaterals are normally lettered counter-clockwise, and PS is a
diameter, the quadrilateral must be inscribed in a semi-circle. I will need
some right triangles so I will bisect everything including the diameter. The
green line segments are the perpendicular bisectors of the upper 3 sides and
the angles as well since the triangles are isosceles. So the radius of the
circle is u/2, and will be the hypotenuse of all 6 right triangles in this figure:
 [eqs. A]
[eqs. A]  and and  The sum of all 6 angles is 180o
The sum of all 6 angles is 180o

 2α and β are complementary,
2α and β are complementary,
 α and α+β are also complementary
So
α and α+β are also complementary
So  [eq. B]
[eq. B] 
 . Taking sines of both sides: . Taking sines of both sides:


 Using the associative law and since 2α and β are complementary,
Using the associative law and since 2α and β are complementary,
 Substituting from [eq. B] above
Substituting from [eq. B] above

 From [eqs. A]
From [eqs. A]

 Multiply through by u3
Multiply through by u3

 Since
Since 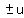 are factors of the last term, we try both and
find that w=-u is a solution and so we factor it by synthetic
division
-u | u 2v2 2uv2-u3
| -u2 -2uv2+u3
u 2v2-u2 0 are factors of the last term, we try both and
find that w=-u is a solution and so we factor it by synthetic
division
-u | u 2v2 2uv2-u3
| -u2 -2uv2+u3
u 2v2-u2 0

 ; ; 
 ; ; 


 So the term
So the term  must be an integer, since the terms
on the right are integers.
For contradiction, assume u is a prime number.
If u=2, then the radius is 1, and the semicircle is π.
So must be an integer, since the terms
on the right are integers.
For contradiction, assume u is a prime number.
If u=2, then the radius is 1, and the semicircle is π.
So 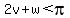 , that would make v=1, w=2. then triangle
SRO would have sides 1,1,2 which violates the triangle
inequality. So u is not the prime number 2.
Thus u must divide evenly into v2. But if u is a prime
then u must divide evenly into v as well. This cannot be true
because v < u, the diameter.
Thus we have a contradiction and u cannot be a prime number.
Edwin , that would make v=1, w=2. then triangle
SRO would have sides 1,1,2 which violates the triangle
inequality. So u is not the prime number 2.
Thus u must divide evenly into v2. But if u is a prime
then u must divide evenly into v as well. This cannot be true
because v < u, the diameter.
Thus we have a contradiction and u cannot be a prime number.
Edwin
Question 1192638: Write the missing statement and reasons to complete the proof.
Given: 𝑁𝑂 ∥ 𝑀𝑃, ∠𝑁 ≅ ∠𝑃
Prove: 𝑀𝑁 ∥ 𝑂𝑃
( square with N on top left and O on top right, then M on bottom left and P on bottom right ) With a dash line going from M to O
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In triangle MNO and MPO
angle N = angle P (given)
Angle NOM = angle PMO ( alternate angles )
MO is common to both triangles
Therefore triangle POM congruent to triangle NMO
So angle POM is congruent to angle NMO .
But they are alternate angles between lines MN and OP
SO MN ||OP

Proved
Question 1179588: https://ibb.co/vwTrxgh
(Please copy paste the link to view the figure)
Given: JA = JL; JC bisects Angle AJL
Prove: KC bisects Angle AKL
Thank you :)
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! In triangle AJK and LJK
AJ = JL given
1=2 (given)
JK common side
Therefore triangle AJK and LJK are congruent (by SAS test)
Triangle AKJ is congruent to LKJ ( congruent angles of congruent triangles)
Therefore 5=6
Therefore KC bisects Angle AKL
 . .
Question 1206239: Given:
RS ⊥ ST
RS ⊥ SQ
∠STR ≅ ∠SQR
Prove:
△RST ≅ △RSQ
STATEMENT REASON
1.RS ⊥ ST, RS ⊥ SQ, ∠STR ≅ ∠SQR 1.
2. 2.
3. 3.
4. △RST ≅ △RSQ 4.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! STATEMENT ..............................................................REASON
1.RS ⊥ ST, RS ⊥ SQ, ∠STR ≅ ∠SQR ..............................given
2. QT ≅ RS ...........................................................Reflective Property
3. QR ≅ TS.......................................................... Reflective property
4. △RST ≅ △RSQ .................................................... SSS
Question 1206186: Look at the figure below:
Triangle EFD has the measure of angle EFD equal to 60 degrees. G is a point on side DF. Points E and G are joined by a straight
https://api.agilixbuzz.com/Resz/~0.Bv8W_aJ6tRosNuyK.A.WQX-LKs4_7CtNbGXeaKp1TM-Q57bSJTC4440BKyZad8/196638831,F41,1,15,0,30,0,3/Assets/94559_55a90aae/image0044e8cadde.jpg
Make a two-column proof showing statements and reasons to prove that triangle DEF is similar to triangle DGE.
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Question 1206184: In the figure below, ΔABC ≅ ΔDEF. Point C is the point of intersection between segment AG and segment BF , while point E is the point of intersection between segment DG and segment BF.
https://api.agilixbuzz.com/Resz/~0.Bv8W_aJ6tRosNuyK.A.WQX-LKs4_7CtNbGXeaKp1TM-Q57bSJTC4440BKyZad8/196638831,F41,1,15,0,30,0,3/Assets/94559_55a90aae/05_08_1b.gif
The figure shows a polygon comprised of three triangles, ABC, CEG, and DFE.
Prove ΔABC ∼ ΔGEC.
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1206126: Prove by contradiction that the diagonals of a kite intersect at right angles? My proof is very wordy,can you help me be more precise. Thank you
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Question 1206134: Prove 𝐶−𝐷=𝐶∩𝐷'. Just having a little bit of trouble with my wording of the proof. Thank you.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x be an element of the set 𝐶−𝐷.
It means that x does belong to C and does not belong to D.
In other words, x does belong to C and does belong to D'.
Hence, x belongs to the intersection 𝐶∩𝐷'.
+----------------------------------------------+
| Thus we proved that |
| the set C-D is the subset of the set 𝐶∩𝐷'. |
+--------------------------------------------- +
In opposite, if x is an element of the set 𝐶∩𝐷',
then x does belong to C and does belong to D'.
It means that x does belong to C and does not belong to D.
In other words, x does belong to the set C-D.
Hence, x belongs to 𝐶∩𝐷'.
+-----------------------------------------------+
| Thus we proved that |
| the set 𝐶∩𝐷' is the subset of the set C-D. |
+-----------------------------------------------+
It implies that C-D = 𝐶∩𝐷'.
At this point, the proof is complete.
Question 1206128: Write a coordinate proof to show that the segments connecting the midpoints of any quadrilateral form a parallelogram. I think it is simpler to use vectors but not sure if I have to use midpoint formulas. Thank you.
Answer by greenestamps(13200)   (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690
|






 .
.