Question 1208064: Quadrilateral PQRS is cyclic and side PS = u is a
diameter of the circle. If PQ = QR = v, RS = w, and u, v,
and w are integers such that v does not equal w, prove that u cannot be a
prime number.
Found 5 solutions by Edwin McCravy, mccravyedwin, AnlytcPhil, Plocharczyk, ikleyn:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Maybe Ikleyn or Greenestamps can simplify my solution but here it is at last.
Since quadrilaterals are normally lettered counter-clockwise, and PS is a
diameter, the quadrilateral must be inscribed in a semi-circle. I will need
some right triangles so I will bisect everything including the diameter. The
green line segments are the perpendicular bisectors of the upper 3 sides and
the angles as well since the triangles are isosceles. So the radius of the
circle is u/2, and will be the hypotenuse of all 6 right triangles in this figure:
 [eqs. A]
[eqs. A]  and and  The sum of all 6 angles is 180o
The sum of all 6 angles is 180o

 2α and β are complementary,
2α and β are complementary,
 α and α+β are also complementary
So
α and α+β are also complementary
So  [eq. B]
[eq. B] 
 . Taking sines of both sides: . Taking sines of both sides:


 Using the associative law and since 2α and β are complementary,
Using the associative law and since 2α and β are complementary,
 Substituting from [eq. B] above
Substituting from [eq. B] above

 From [eqs. A]
From [eqs. A]

 Multiply through by u3
Multiply through by u3

 Since
Since 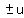 are factors of the last term, we try both and
find that w=-u is a solution and so we factor it by synthetic
division
-u | u 2v2 2uv2-u3
| -u2 -2uv2+u3
u 2v2-u2 0 are factors of the last term, we try both and
find that w=-u is a solution and so we factor it by synthetic
division
-u | u 2v2 2uv2-u3
| -u2 -2uv2+u3
u 2v2-u2 0

 ; ; 
 ; ; 


 So the term
So the term  must be an integer, since the terms
on the right are integers.
For contradiction, assume u is a prime number.
If u=2, then the radius is 1, and the semicircle is π.
So must be an integer, since the terms
on the right are integers.
For contradiction, assume u is a prime number.
If u=2, then the radius is 1, and the semicircle is π.
So 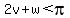 , that would make v=1, w=2. then triangle
SRO would have sides 1,1,2 which violates the triangle
inequality. So u is not the prime number 2.
Thus u must divide evenly into v2. But if u is a prime
then u must divide evenly into v as well. This cannot be true
because v < u, the diameter.
Thus we have a contradiction and u cannot be a prime number.
Edwin , that would make v=1, w=2. then triangle
SRO would have sides 1,1,2 which violates the triangle
inequality. So u is not the prime number 2.
Thus u must divide evenly into v2. But if u is a prime
then u must divide evenly into v as well. This cannot be true
because v < u, the diameter.
Thus we have a contradiction and u cannot be a prime number.
Edwin
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
Answer by Plocharczyk(17)   (Show Source): (Show Source):
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Quadrilateral PQRS is cyclic and side PS = u is a
diameter of the circle. If PQ = QR = v, RS = w, and u, v,
and w are integers such that v does not equal w, prove that u cannot be a
prime number.
~~~~~~~~~~~~~~~~~~~~~~~~
I will give another solution, different from Edwin, and more compact.
Make a sketch.
So, you have quadrilateral PQRS inscribed in the circle such that PS
is a diameter of this circle; PQ = QR = v; RS = w; PS = u.
Draw the diagonal PR. Let PR = d (the length).
We have isosceles triangle PQR. Using the cosine law, we can write
 = = 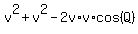 or
or
 = = 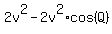 . (1)
From the other hand, triangle PRS is the right triangle, since angle PRS
leans on the diameter PS. Therefore, . (1)
From the other hand, triangle PRS is the right triangle, since angle PRS
leans on the diameter PS. Therefore,
 = = 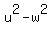 . (2)
From (1) and (2), we can exclude . (2)
From (1) and (2), we can exclude  and write and write
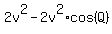 = = 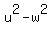 . (3)
Since quadrilateral PQRS is inscribed in the circle, its opposite angles S and Q
are supplementary: S + Q = . (3)
Since quadrilateral PQRS is inscribed in the circle, its opposite angles S and Q
are supplementary: S + Q =  . Therefore, cos(Q) = -cos(S).
Hence, from (3) we have . Therefore, cos(Q) = -cos(S).
Hence, from (3) we have
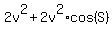 = = 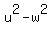 . (4)
Next, cos(S) = . (4)
Next, cos(S) =  (from the right triangle PRS).
Thus (from the right triangle PRS).
Thus
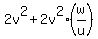 = = 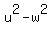 . (5)
Multiply both sides of (5) by "u". You will get . (5)
Multiply both sides of (5) by "u". You will get
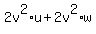 = = 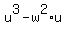 .
Combine the terms with "u" on the right side; keep the remaining term .
Combine the terms with "u" on the right side; keep the remaining term 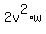 on the left side on the left side
 = = 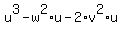 . (6)
In (6), right side is a multiple of "u". So, if "u" is a prime number,
then left side . (6)
In (6), right side is a multiple of "u". So, if "u" is a prime number,
then left side 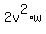 is a multiple of "u".
Hence, EITHER "u" divides 2, OR "u" divides is a multiple of "u".
Hence, EITHER "u" divides 2, OR "u" divides  , OR "u" divides "w".
It leads to contradiction, since
- if "u" divides 2, then u= 2; but then from the right triangle PRS the leg w
must be shorter than the hypotenuse u, i.e. w= 1; and side v must be shorter
than the diameter u= 2; so, in this case w = v, which is excluded in the problem.
- if "u" divides , OR "u" divides "w".
It leads to contradiction, since
- if "u" divides 2, then u= 2; but then from the right triangle PRS the leg w
must be shorter than the hypotenuse u, i.e. w= 1; and side v must be shorter
than the diameter u= 2; so, in this case w = v, which is excluded in the problem.
- if "u" divides  , then "u" divides "v"; but it is impossible, since
"v" is less than "u" (the diameter).
- if "u" divides "w", it is also impossible, since "w" is less than "u" (the diameter).
These contradictions prove that "u" can not be a prime number. , then "u" divides "v"; but it is impossible, since
"v" is less than "u" (the diameter).
- if "u" divides "w", it is also impossible, since "w" is less than "u" (the diameter).
These contradictions prove that "u" can not be a prime number.
Solved.
|
|
|