Tutors Answer Your Questions about Geometry proofs (FREE)
Question 1168388: A cat has thirteen kittens. Eight of the kittens have white hair, six of the kittens have spots, and eight of the kittens have long tails. All of the kittens have at least one of these traits. One kitten is white with spots and a long tail. Three of the kittens are white with spots. Two kittens have spots and long tails. One kitten has white hair but does not have spots or a long tail.
A. Draw a Venn diagram for this problem.
B. How many kittens are white with long tails, but don't have spots?
Thank you
Click here to see answer by CPhill(1959)   |
Question 1169211: Given that ∠FAB≅∠GED and C is the midpoint of AE¯¯¯¯¯, which of the following proves that △ABC≅△EDC?
https://thinkwell.cachefly.net/questionbank/95001-96000/95608/img/95608a.svg
A.
1. ∠FAB≅∠GED (Given)2. ∠BAC is the supp. of ∠FAB; ∠DEC is thesupp. of ∠GED (Def. of Supp. ∠s)3. ∠BAC≅∠DEC (≅ Supp. Thm.)4. ∠ACB≅∠DCE (Vert. ∠s Thm.)5. C is the midpoint of AE¯¯¯¯¯ (Given)6. AC¯¯¯¯¯≅EC¯¯¯¯¯ (Def. of mdpt.)7. △ABC≅△EDC (by ASA Steps 3, 6, 4)
B.
1. ∠FAB≅∠GED (Given)2. ∠BAC is the supp. of ∠FAB; ∠DEC is thesupp. of ∠GED (Def. of Supp. ∠s)3. ∠BAC≅∠DEC (≅ Supp. Thm.)4. ∠ACB≅∠DCE (Adj. ∠s Thm.)5. C is the midpoint of AE¯¯¯¯¯ (Given)6. AC¯¯¯¯¯≅EC¯¯¯¯¯ (Def. of mdpt.)7. △ABC≅△EDC (by ASA Steps 3, 6, 4)
C.
1. ∠FAB≅∠GED (Given)2. ∠BAC is the supp. of ∠FAB; ∠DEC is thesupp. of ∠DEG (Def. of Supp. ∠s)3. BC¯¯¯¯¯≅CD¯¯¯¯¯ (≅ Supp. Thm.)4. ∠ACB≅∠BCE (Vert. ∠s Thm.)5. C is the midpoint of AE¯¯¯¯¯ (Given)6. BC¯¯¯¯¯≅CD¯¯¯¯¯ (Def. of mdpt.)7. △ABC≅△EDC (by SAS Steps 3, 1, 6)
D.
1. ∠FAB≅∠GED (Given)2. ∠BAC is the supp. of ∠FAB; ∠DEC is thesupp. of ∠GED (Def. of Supp. ∠s)3. BC¯¯¯¯¯≅CD¯¯¯¯¯ (≅ Supp. Thm.)4. ∠ACB≅∠BCE (Vert. ∠s Thm.)5. C is the midpoint of AE¯¯¯¯¯ (Given)6. BC¯¯¯¯¯≅CD¯¯¯¯¯ (Def. of mdpt.)7. △ABC≅△EDC (by SAS Steps 3, 1, 6)
Click here to see answer by CPhill(1959)   |
Question 1170173: I have two right triangles that are connected at point x. On the right, there is triangle one which has point v at the top, w at the corner, and x which connects to triangle two which has point z at the bottom, connected to y which connects to x.
I am given that line WV is perpendicular to line WY. I am also given that line ZY is perpendicular to line WY, as well as line WV is congruent to ZY. I am supposed to prove that the triangles are congruent and X is the midpoint of line VZ.
I do have a 4th statement that I attempted to do. That is that angle W is congruent to angle Y because of the def. of perpendicularity. I also have about half of the fifth statement which is that angle 1 and angle 2 are congruent. I don't know how to prove this with reason. I need help.
Click here to see answer by CPhill(1959)   |
Question 1173654: Provide a two column proof or paragraph proof.
Given MA and AI are perpendicular: RS and AI are perpendicular : K is the midpoint of MT.
Prove: Triangles MAK and TIK are congruent. (If didn't work prove Triangles MKI and TKA are congruent)
Click here to see answer by CPhill(1959)   |
Question 1175420: Suppose 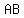 and and 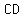 are two non-intersecting chords of a circle. Take any point are two non-intersecting chords of a circle. Take any point  on the on the
arc 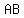 not containing not containing 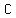 , , 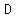 . Let . Let 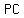 and and  intersect intersect 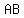 at at  , ,  respectively. Show respectively. Show
that AQ×RB/QR
is constant (irrespective of position of  ). ).
Click here to see answer by CPhill(1959)   |
Question 1182026: A student tried to trisect an angle G using the following procedure:
1. Mark off GA congruent to GB.
2. Draw AB
3. Divide AB into 3 congruent parts so that AX=XY=YB.
4. Draw GX and GY.
Show that the student did not trisect angle G (Hint: Show that GA>GY. Then use indirect proof to show that angle XGY is not equal to angle XGA.)
I know how to show that GA>GY (by SAS Inequality) but cannot show why angle XGY is not equal to angle XGA using indirect proof. I appreciate any help! Thanks in advance!
Click here to see answer by Edwin McCravy(20056)   |
Question 1182026: A student tried to trisect an angle G using the following procedure:
1. Mark off GA congruent to GB.
2. Draw AB
3. Divide AB into 3 congruent parts so that AX=XY=YB.
4. Draw GX and GY.
Show that the student did not trisect angle G (Hint: Show that GA>GY. Then use indirect proof to show that angle XGY is not equal to angle XGA.)
I know how to show that GA>GY (by SAS Inequality) but cannot show why angle XGY is not equal to angle XGA using indirect proof. I appreciate any help! Thanks in advance!
Click here to see answer by CPhill(1959)   |
Question 1181982: Given: angle QPS is equal and congruent to angle TPR
Prove: angle QPR is equal and congruent to angle TPS.
The diagram has angle QPT divided into 3 smaller angles.
Left: QPR
Interior: RPS
Right: SPT
The interior angle RPS is significantly larger than the 2 exterior angles QPR and SPT.
1.angle QPS =& congruent angle TPR. Given
2.m angle QPS = m angle TPR. Definition. of congruence
3.m angle QPS = m angle QPR + m angle RPS. Angle addition
m angle TPR = m angle TPS + m angle RPS. postulate
4. ____________________________. Substitution
5._______________________________. ________________
6. Angle QPR =&congruent to angle TPS. __________________
Click here to see answer by CPhill(1959)   |
Question 1182025: A student tried to trisect an angle G using the following procedure:
1. Mark off GA congruent to GB.
2. Draw AB
3. Divide AB into 3 congruent parts so that AX=XY=YB.
4. Draw GX and GY.
Show that the student did not trisect angle G (Hint: Show that GA>GY. Then use indirect proof to show that m
I know how to show that GA>GY (by SAS Inequality) but cannot show why m
Click here to see answer by CPhill(1959)   |
Question 1182497: Consider two points A and B, whose position vectors are a and b. The angle bisector of AOB meets AB at X. Let vector OX = u(a+b). Similarly, let vector AX = d(AB),where 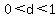 . Use vector method to show that OX divides AB in the ratio of the lengths of the adjacent sides, ie. AX:XB = OA:OB . Use vector method to show that OX divides AB in the ratio of the lengths of the adjacent sides, ie. AX:XB = OA:OB
Click here to see answer by CPhill(1959)   |
Question 1191529: Draw a triangle with vertices A(0, 4), B(2, -2), and C(-2, -2). Apply a dilation centered at the origin with scale factor to this triangle and draw the resulting triangle,A'B'C'. In complete sentences, describe the following:
The relationship between corresponding sides in terms of their lengths.
The relationship between corresponding sides in terms of their orientations.
The relationship between corresponding angles in terms of their measures.
Click here to see answer by CPhill(1959)   |
Question 1191473: In a word processing document or on a separate piece of paper, use the guide to construct a two column proof proving that triangle RST is congruent to triangle RSQ given that RS ⊥ ST, RS ⊥ SQ, and ∠STR ≅ ∠SQR. Submit the entire proof to your instructor.
Given:
RS ⊥ ST
RS ⊥ SQ
∠STR ≅ ∠SQR
Prove:
△RST ≅ △RSQ
STATEMENT REASON
1.RS ⊥ ST, RS ⊥ SQ, ∠STR ≅ ∠SQR 1.
2. 2.
3. 3.
4. △RST ≅ △RSQ 4.
Click here to see answer by CPhill(1959)   |
Question 1208294: 1. If A, B, C, D are collinear and AB = 8, AC = 12, AD = 16, BC = 20,
BD = 24, CD = 28, find all possible betweenness relations.
2.Show that if A ∗ B ∗ C and B ∗ C ∗ D, then A ∗ B ∗ D and A ∗ C ∗ D.
[5]
Click here to see answer by ikleyn(52788)   |
Question 1192638: Write the missing statement and reasons to complete the proof.
Given: 𝑁𝑂 ∥ 𝑀𝑃, ∠𝑁 ≅ ∠𝑃
Prove: 𝑀𝑁 ∥ 𝑂𝑃
( square with N on top left and O on top right, then M on bottom left and P on bottom right ) With a dash line going from M to O
Click here to see answer by mananth(16946)   |
Question 1206186: Look at the figure below:
Triangle EFD has the measure of angle EFD equal to 60 degrees. G is a point on side DF. Points E and G are joined by a straight
https://api.agilixbuzz.com/Resz/~0.Bv8W_aJ6tRosNuyK.A.WQX-LKs4_7CtNbGXeaKp1TM-Q57bSJTC4440BKyZad8/196638831,F41,1,15,0,30,0,3/Assets/94559_55a90aae/image0044e8cadde.jpg
Make a two-column proof showing statements and reasons to prove that triangle DEF is similar to triangle DGE.
Click here to see answer by mccravyedwin(407)   |
Question 1206184: In the figure below, ΔABC ≅ ΔDEF. Point C is the point of intersection between segment AG and segment BF , while point E is the point of intersection between segment DG and segment BF.
https://api.agilixbuzz.com/Resz/~0.Bv8W_aJ6tRosNuyK.A.WQX-LKs4_7CtNbGXeaKp1TM-Q57bSJTC4440BKyZad8/196638831,F41,1,15,0,30,0,3/Assets/94559_55a90aae/05_08_1b.gif
The figure shows a polygon comprised of three triangles, ABC, CEG, and DFE.
Prove ΔABC ∼ ΔGEC.
Click here to see answer by MathLover1(20850)   |
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690
|




