Question 805916: HELP! The directions say that there is more information than is needed. We are to state the one piece of information that is not needed then do a two column proof that does not use that information.
Given: Segment LM is congruent to segment LN
Segment KM is congruent to segment KN
Ray KO bisects angle MKN
Prove LO bisects angle MLN
Thanks in advance!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Unless more information is given in a figure, I do not see any superfluous, unneeded information.
Maybe there was a figure that you could not include in your post.
If you remove the statement "Segment LM is congruent to segment LN",
I do not even know that a point named L exists.
If you remove the statement "Segment KM is congruent to segment KN",
I do not even know that a point named N exists.
If you remove the statement "Ray KO bisects angle MKN",
I do not even know that a point named O exists.
If you tell me that there is a picture that shows a quadrilateral KLMN,
such as the ones drawn in black below (or maybe a rotated version),
with diagonals (or extended diagonals) like the ones drawn in green below,
  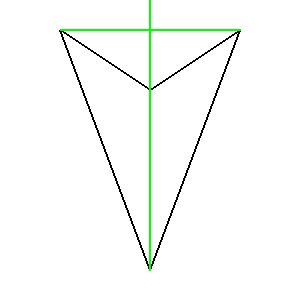
and the intersection of the diagonals is point O,
then "Ray KO bisects angle MKN" is not needed.
In that case, you would know that triangles MKN and MLN
are isosceles triangles, sharing side MN as their potentially unequal side.
You could prove that those diagonals split the quadrilateral into congruent triangles, and they split each isosceles triangle into two congruent right triangles.
That would prove
"Ray KO bisects angle MKN" and
"Ray LO bisects angle MLN",
as least regarding the acute angles with those names.
The constructions that are usually taught early in geometry class to to draw the bisector of an angle or the perpendicular bisector of a segment are all based on this.
In a better world, all teachers that show that construction (from elemntary school to college) would explain what it's based on, and all students would know it.
|
|
|