If the black triangle below is isosceles, and the vertices of the green
triangle are the midpoints of the sides of the black triangle, that the
green triangle is also isosceled:
 Since the black triangle is isosceles we can let it be triangle PQR,
where the vertices are P(0,b), Q(-a,0), and R(a,0), where a and b are
both positive numbers:
Since the black triangle is isosceles we can let it be triangle PQR,
where the vertices are P(0,b), Q(-a,0), and R(a,0), where a and b are
both positive numbers:
 Now we will let S, T. and U be the midpoints respectively of
PQ, PR and QR.
We will use the midpoint formula to find the coordinates of S,T, and U:
For S:
Midpoint =
Now we will let S, T. and U be the midpoints respectively of
PQ, PR and QR.
We will use the midpoint formula to find the coordinates of S,T, and U:
For S:
Midpoint = 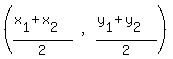 Midpoint of PQ = S
Midpoint of PQ = S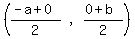 Midpoint of PQ = S
Midpoint of PQ = S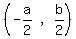 For T:
Midpoint =
For T:
Midpoint = 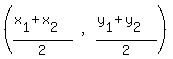 Midpoint of PR = T
Midpoint of PR = T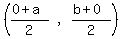 Midpoint of PR = T
Midpoint of PR = T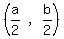 For U:
Midpoint =
For U:
Midpoint = 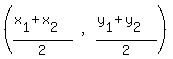 Midpoint of QR = U
Midpoint of QR = U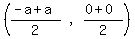 Midpoint of QR = U(0,0)
Midpoint of QR = U(0,0)
 Now all we need is to show that US = UT.
We will use the distance tance formula to show that:
d =
Now all we need is to show that US = UT.
We will use the distance tance formula to show that:
d = 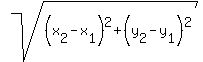 SU =
SU = 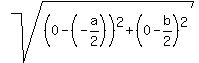 SU =
SU = 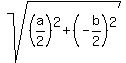 SU =
SU =  SU =
SU = 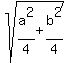 SU =
SU =  SU =
SU = 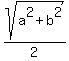 d =
d = 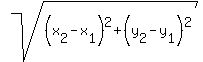 TU =
TU = 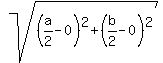 TU =
TU = 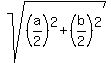 TU =
TU =  TU =
TU = 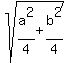 TU =
TU =  TU =
TU = 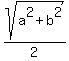 So SU = TU and therefore triangle STU is isosceles.
Edwin
So SU = TU and therefore triangle STU is isosceles.
Edwin