Question 161720: show that the quadrilateral formed by joining the mid-points of the sides of a square is also a square.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given:
 , ,  , ,  and and 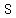 are the are the of of  , ,  , ,  and and 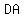 respectively. respectively.
To prove:
 is is  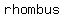 . .
Proof:
Consider triangle 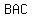
 || ||  and and  ….(1) ….(1)
(In a triangle the segment joining the mid-points of
two sides are parallel and equal to third side)
Consider triangle 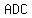 , ,
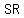 || ||  and and  ….(2) ….(2)
From (1) and (2),
 || || 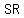 and and 
 is a parallelogram ……………….(3) is a parallelogram ……………….(3)
 ….. (opposite sides of a rectange) ….. (opposite sides of a rectange)
So
 ….. …..
i.e. 
Consider triangle 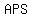 , and triangle , and triangle  , ,
 …. ( …. ( is the mid-point of is the mid-point of  ) )

angle 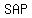 = = 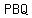 = = 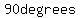
So,  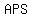 is is 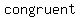 to triangle to triangle  .... ( .... (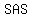 congruency condition) congruency condition)
 ………………………..(4) ………………………..(4)
From (3) and (4),
 is a parallelogram in which is a parallelogram in which  . .
 is a is a 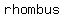 . .
|
|
|