SOLUTION: Given: Quadrilateral ABCD; Angle A is conguent to Angle C; Angle B is congruent to Angle D Prove: Quadrilateral ABCD is a Parallelogram.

          D___________________ C
          /&               # /
         /                  /
        /                  /
     A /#                &/B
       ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ 

Given: Quadrilateral ABCD
       
1. mÐA = mÐC
   mÐB = mÐD                     They are measures of congruent angles.   

mÐA + mÐB + mÐC + mÐD = 360°     The sum of the measures of the interior 
                                 angles of a polygon with n sides has sum
                                 of angles given by the expression
                                 °. Quadrilaterals have 4 
                                 sides, which means that n=4. Therefore 
                                 the sum of the interior angles of a  
                                 quadrilateral is ° which
                                 equals 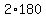° or °

mÐA + mÐB + mÐA + mÐB = 360°     Equals may be substituted for equals. Here
                                 we are given that mÐA = mÐC and that 
                                 mÐB = mÐD, and we made those substitutions
                                 of equals for equals. 

2mÐA + 2mÐB = 360°               mÐA + mÐA = 2AÐ and mÐB + mÐB = 2ÐB and
                                 substituting equals for equals.

 mÐA + mÐB = 180°                Dividing the equation through by 2.
(ÐA and ÐB are supplementary)  

AD||BC                           When a transversal (AB) cuts two lines
                                 (AD and BC), and the angles on the same
                                 side of the transversal (ÐA and ÐB) are
                                 suplementary, the lines are parallel.

m/C + m/B = 180°                 Substituting mÐC for mÐA in equation 2 steps back.     
(ÐC and ÐB are supplementary)

AB||CD                           When a transversal (BC) cuts two lines
                                 (AB and CD), and the angles on the same
                                 side of the transversal (ÐC and ÐB) are
                                 suplementary, the lines are parallel.

quadrilateral ABCD is a parallellogram.
                       
                                 Because both pairs of opposite sides are
                                 parallel and that completes the definition 
                                 of a parallelogram.   

Edwin