Question 1210551: In equiangular octagaon EFGHIJKL, we know that EF = GH = IJ = KL = 1 and FG = HI = JK = LE = sqrt(2). Find the area of the octagon.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3833)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 7 square units
Explanation
On a piece of graph paper, plot the points
P = (0,0)
Q = (3,0)
R = (3,3)
S = (0,3)
This forms square PQRS which has area 3^2 = 9 square units.
We'll use this value later.
Contained in this square will be octagon EFGHIJKL.
We'll place the vertices at the following locations
E = (1, 0)
F = (2, 0)
G = (3, 1)
H = (3, 2)
I = (2, 3)
J = (1, 3)
K = (0, 2)
L = (0, 1)
For horizontal or vertical segments, such as EF, you can simply count the number of spaces between the points to find the segment lengths.
The distance formula could be used, but it would be overkill.
You should find all horizontal and vertical segments are 1 unit each.
For diagonal pieces, use either the Distance Formula or the Pythagorean Theorem.
Each diagonal piece is sqrt(2) units long.
You should find that each interior angle of the octagon is 135 degrees, which proves it to be equiangular. It's not regular since the sides aren't the same length.
Let's return to square PQRS.
We need to clip a right triangle from each corner to form octagon EFGHIJKL.
One such triangular piece to clip off would be triangle ELP, which has area = base*height/2 = 1*1/2 = 0.5
Four such congruent pieces to clip off would mean a total of 4*0.5 = 2 square units are removed.
Therefore octagon EFGHIJKL has area 9-2 = 7 square units
Answer by ikleyn(53646)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In equiangular octagon EFGHIJKL, we know that EF = GH = IJ = KL = 1 and FG = HI = JK = LE = sqrt(2).
Find the area of the octagon.
~~~~~~~~~~~~~~~~~~~~~~~~~
Let's write the sequence of side lengths in the row
EF FG GH HI IJ JK KL LE
1 sqrt(2) 1 sqrt(2) 1 sqrt(2) 1 sqrt(2) <<<---=== (1)
You see the repeating pattern as a cycle.
All interior angles are 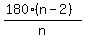 = = 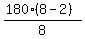 = = 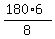 = = 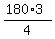 = 45*3 = 135 degrees.
You can calculate the length of the diagonal EG using the cosine law formula = 45*3 = 135 degrees.
You can calculate the length of the diagonal EG using the cosine law formula
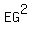 = = 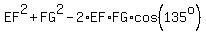 = = 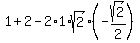 = = 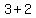 = 5.
so EG = = 5.
so EG = 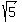 .
Obviously, all such sides EG, GI, IK and KE have the same length .
Obviously, all such sides EG, GI, IK and KE have the same length 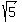 due to the same reason (the same logic).
Next, this octagon has a remarkable symmetry: if you rotate it in a way that vertex E goes to vertex G
E ---> G,
then the new octagon (the image under this rotation) will coincide with the original octagon.
(simply because the sequence of side lengths (1) will be the same and all interior angles are congruent).
It means that the quadrilateral FHJK will map into and onto itself.
It means that this quadrilateral is a square.
If such reasoning confuses you, you can notice that sides FH and HJ of the quadrilateral FHJK are orthogonal
since two times angle 135 degs is 270 degs. And, similarly, quadrilateral FHJK has all his consecutive sides
orthogonal with equal lengths, so this quadrilateral is a square.
Now, the area of the square FHJK is the square of its side, i.e. due to the same reason (the same logic).
Next, this octagon has a remarkable symmetry: if you rotate it in a way that vertex E goes to vertex G
E ---> G,
then the new octagon (the image under this rotation) will coincide with the original octagon.
(simply because the sequence of side lengths (1) will be the same and all interior angles are congruent).
It means that the quadrilateral FHJK will map into and onto itself.
It means that this quadrilateral is a square.
If such reasoning confuses you, you can notice that sides FH and HJ of the quadrilateral FHJK are orthogonal
since two times angle 135 degs is 270 degs. And, similarly, quadrilateral FHJK has all his consecutive sides
orthogonal with equal lengths, so this quadrilateral is a square.
Now, the area of the square FHJK is the square of its side, i.e. 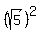 = 5.
Now you can calculate the area of triangle EFG = 5.
Now you can calculate the area of triangle EFG
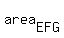 = = 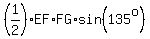 = = 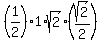 = = 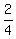 = =  .
We have 4 such triangles as EFG, so their total area is .
We have 4 such triangles as EFG, so their total area is 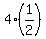 = 2.
Now the total area of the octagon EFGHIJKL is the sum of the area of square FHGK PLUS four triangles
5 + 2 = 7.
At this point, the solution is complete.
The area of the octagon EFGHIJKL is 7 square units. ANSWER = 2.
Now the total area of the octagon EFGHIJKL is the sum of the area of square FHGK PLUS four triangles
5 + 2 = 7.
At this point, the solution is complete.
The area of the octagon EFGHIJKL is 7 square units. ANSWER
Solved.
Nice problem. It is a fun to solve it.
|
|
|