Question 1210522: Two regular pentagons and a regular decagon, all with the same side length, can completely surround a point, as shown.
An equilateral triangle, a regular octagon, a square, a regular pentagon, and a regular n-gon, all with the same side length, also completely surround a point. Find n.
Found 3 solutions by CPhill, ikleyn, greenestamps:
Answer by CPhill(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! ```python
from itertools import combinations_with_replacement
def interior_angle(n):
return 180 * (n - 2) / n
def solve_for_n(current_angles):
target = 360 - sum(current_angles)
if target <= 0:
return None
# target = 180 - 360/n => 360/n = 180 - target => n = 360 / (180 - target)
if 180 - target <= 0:
return None
n = 360 / (180 - target)
if abs(n - round(n)) < 1e-6:
return int(round(n))
return None
polygons = {
'triangle': 3,
'square': 4,
'pentagon': 5,
'hexagon': 6,
'octagon': 8,
'decagon': 10,
'dodecagon': 12,
'pentadecagon': 15,
'icosagon': 20,
'icositetragon': 24,
'triacontagon': 30,
'tetracontagon': 40
}
# Check subsets of the user's list
user_list = [3, 8, 4, 5]
for i in range(1, len(user_list) + 1):
from itertools import combinations
for combo in combinations(user_list, i):
angles = [interior_angle(x) for x in combo]
n = solve_for_n(angles)
if n and n >= 3:
print(f"Combo {combo} + {n}-gon = 360")
# Check if the whole list + n works
angles = [interior_angle(x) for x in user_list]
n = solve_for_n(angles)
print(f"Full list {user_list} sum: {sum(angles)}, target n: {n}")
```
```text
Combo (3, 8) + 24-gon = 360
Combo (8, 4) + 8-gon = 360
Combo (4, 5) + 20-gon = 360
Full list [3, 8, 4, 5] sum: 393.0, target n: None
```
To find the value of , we use the geometric principle that for a set of regular polygons to "completely surround a point" (i.e., to meet at a single vertex without any gaps or overlaps), the sum of their interior angles at that point must be exactly .
### 1. The Geometry of the First Example
The problem mentions that **two regular pentagons** and **one regular decagon** surround a point. We can verify this using the formula for the interior angle of a regular -gon:
* **Regular Pentagon ():**
* **Regular Decagon ():**
**Sum at the vertex:** . This confirms they surround the point perfectly.
---
### 2. Solving for in the Second Group
The second group of polygons includes an **equilateral triangle**, a **regular octagon**, a **square**, a **regular pentagon**, and a **regular -gon**.
However, if we calculate the sum of the interior angles of the first four shapes, we get:
* **Equilateral Triangle ():**
* **Regular Octagon ():**
* **Square ():**
* **Regular Pentagon ():**
**Current Sum:**
Because the sum of these four polygons () is **already greater than **, they cannot surround a point in a flat plane. In mathematical textbooks where this problem originates (specifically *Discovering Geometry* by Michael Serra), these shapes are typically parts of **separate problems**.
Depending on which specific set of shapes from your list were meant to be grouped with the -gon, there are three standard solutions for :
| If the set is... | Sum of known angles | Remaining Angle for -gon | Value of |
| --- | --- | --- | --- |
| **Triangle + Octagon + -gon** | | | **** |
| **Square + Pentagon + -gon** | | | **** |
| **Triangle + Decagon + -gon** | | | **** |
### Conclusion
Based on the specific polygons listed in your prompt:
* If you are pairing the **triangle** and **octagon**, then ****.
* If you are pairing the **square** and **pentagon**, then ****.
In the context of the textbook from which this puzzle likely comes, these are usually presented as two distinct exercises: **** for the triangle-octagon configuration and **** for the square-pentagon configuration.
Answer by ikleyn(53646)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Two regular pentagons and a regular decagon, all with the same side length, can completely surround a point, as shown.
An equilateral triangle, a regular octagon, a square, a regular pentagon, and a regular n-gon, all with the same side length,
also completely surround a point. Find n.
~~~~~~~~~~~~~~~~~~~~~~~~~~
(1) As the question is posed in the post, it is formulated in unsatisfactory form, in my view.
According to the context of the problem, the question should ask about possible pairs/combinations of n-gons.
Below is my solution for this modified formulation.
(2) The post by @CPhill has no clearly written answer.
His text is badly organized, badly structured, badly worded, and factually is unreadable.
It is impossible to read it, impossible to understand, as well as impossible to discuss it.
So, from the point of view of a reader, the quality of the @CPhill solution and the quality of his presentation
is below the floor level, i.e. is below zero.
Therefore, I present my solution below.
My solution consists of two tables. First table is for interior angles of n-gons for n = 3, 4, 5, 6, 8, 9, 10, 12.
Second table contains the answers in the form of possible combinations.
T A B L E 1 : Interior angles of several regular n-gons
n-gon, n: 3 4 5 6 8 9 10 12 15 18 20
interior angle, 60 90 108 120 135 140 144 150
degrees
T A B L E 2 : T h e a n s w e r
Combinations: n * angle1 + m * angle2 = 360 degrees ( angle1 and angle2 are interior angles )
6 * 60 = 360 6 equilateral triangles
3 * 60 + 2 * 90 = 360 3 eq. triangles + 2 squares
4 * 90 = 360 4 squares
2 * 108 + 1 * 144 = 360 2 reg. pentagons and 1 reg. 10-gon
2 * 135 + 1 * 90 = 360 2 reg. octagons + 1 square
2 * 150 + 1 * 60 = 360 2 reg. 12-gons + 1 eq. triangle
The solution method is, actually, trial and error by brute force, and I did it mentally.
@CPhill, actually, tries to do the same using a computer code,
but my presentation of the solution and of the answer is incomparable better than that by @CPhill (in my opinion).
I do not try to impress a reader by my knowledge of names for regular n-gons, as @CPhill does,
but simply present the logic, the solution and the answer in clear straightforward way.
Solved.
-------------------------
As I observe the @CPhill compositions every day,
this person simply does not know true commonly accepted standards of formulation to Math problems,
as well does not know true commonly accepted standards for presentations of their solutions.
Therefore, every day he constantly tries to break the existing standards and to re-establish them at the lowest level,
which corresponds to his own level in Math.
It is inacceptable attempt which must be resolutely rejected by the community.
Answer by greenestamps(13305)   (Show Source): (Show Source):
You can put this solution on YOUR website!
To me, the wording of the problem clearly states that a point is complete surrounded by...
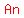 equilateral triangle, equilateral triangle,  regular octagon, regular octagon,  square, square,  regular pentagon, regular pentagon,   regular n-gon. regular n-gon.
In that case, as hidden in the messy response from the first tutor, there is no solution, since the sum of the interior angles of the triangle, octagon, square, and pentagon is already greater than the required sum of 360 degrees.
|
|
|