SOLUTION: In a certain regular polygon, the measure of each interior angle is 2 times the measure of each exterior angle. Find the number of sides in this regular polygon.

In a certain regular polygon, the measure of each interior angle is 2 times the measure of each exterior angle.
Find the number of sides in this regular polygon.

The exterior angles of any polygon, sum to . Therefore, each exterior angle of any regular polygon will be ,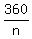
with n being the number of sides

Since it's stated that each interior angle is TWICE each exterior angle, then each interior angle of this regular polygon =  = .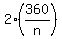

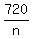Since the 2 angles (interior and exterior) are on a straight line, they are supplementary. This gives us: 
                                                                                                          360 + 720 = 180n ---- Multiplying by LCD, n
                                                                                                              1,080 = 180n
                                                           Number of sides that this regular polygon contains, or 

The regular polygon contains 6 sides, and is therefore, a regular HEXAGON!

OR

Let each exterior angle, be E
Then each interior angle = 2E
As these 2 angles are supplementary, we get: E + 2E = 180
                                                 3E = 180
Measure of each exterior angle of this regular polygon, or E = .
As each exterior angle is , and the sum of the exterior angles of any polygon is , number of sides of this polygon = 
With 6 sides, this makes this a regular HEXAGON!