Question 1210474: In rectangle ABCD, corner A is folded over crease DE to point F on BC. Find BC.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(2103)   (Show Source):
You can put this solution on YOUR website! The problem as stated is **unsolvable** because a necessary dimension is missing. The length of the side $BC$ (which is equal to $AD$) cannot be uniquely determined without knowing the length of the adjacent side **$CD$** (or $AB$).
Here is the general geometric relationship that must hold in this type of folding problem, which shows the dependency:
Let:
* $BC = AD = l$ (The length you are trying to find)
* $CD = w$ (The missing width)
### 1. Relationships from the Fold
When corner $A$ is folded over the crease $DE$ to point $F$ on $BC$, two triangles, $\triangle ADE$ and $\triangle FDE$, are congruent. This gives us the following equivalences:
* The hypotenuse of the fold: $DF = AD = l$
* The fold sides: $AE = FE$
* $\angle DFE = \angle DAE = 90^\circ$
### 2. Using the Pythagorean Theorem
We can set up two equations using the Pythagorean theorem in the right-angled triangles $\triangle FDC$ and $\triangle FCE$:
* **In $\triangle FDC$ (Right-angled at C):**
$$DF^2 = DC^2 + CF^2$$
$$l^2 = w^2 + CF^2 \quad \rightarrow \quad CF = \sqrt{l^2 - w^2}$$
* **In $\triangle FCE$ (Right-angled at C):**
$$FE^2 = CE^2 + CF^2$$
Since $FE = AE$, we substitute $AE$ and the expression for $CF^2$:
$$AE^2 = CE^2 + (l^2 - w^2)$$
### 3. Using the Side $CD$
The line segments $DE$ and $CE$ make up the side $CD$: $CD = DE + CE$.
* **In $\triangle ADE$ (Right-angled at D):**
$$AE^2 = AD^2 + DE^2$$
$$AE^2 = l^2 + DE^2$$
### Conclusion of Dependency
By setting the two expressions for $AE^2$ equal to each other:
$$CE^2 + l^2 - w^2 = l^2 + DE^2$$
$$\rightarrow CE^2 = DE^2 + w^2$$
Since $w$ and $l$ are not given, $BC$ (which is $l$) cannot be uniquely determined.
**To solve the problem, you must know the length of $CD$ (or a relationship between $l$ and $w$).**
Answer by ikleyn(53250)  (Show Source):
You can put this solution on YOUR website! .
In rectangle ABCD, corner A is folded over crease DE to point F on BC. Find BC.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Make a sketch following my descriptions/instructions.
We consider rectangle ABCD. For simplicity, assume that the rectangle is "vertical",
i.e. its vertical dimension 'b' = AD = BC is greater than (or equal to) its horizontal dimension 'a' = AB = CD.
We fold corner A, so point A comes to point F on BC: so, point F is the image of point A
under folding, and F is on BC between points B and C. <<<---=== It is in accordance with the given part.
Then it is clear that at this folding the side AB transforms to interval BF;
so, AB = BF = a.
It is also clear that at this folding the side AD becomes FD; therefore, DF = b.
Consider right-angled triangle FCD. For its leg FC we can write
FC =  =  .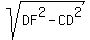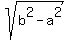
Now interval BC is the sum of two intervals
BC = BF + FC = a +  .
But BC = b; so, we can rewrite the last equation in the form
b = a + . (1)
Now we will perform formal transformations with this equation. From (1) we have, moving 'a' on the left side
b - a = .
Square both sides
(b-a)^2 = b^2 - a^2,
b^2 - 2ab + a^2 = b^2 - a^2
Cancel b^2 in both sides and continue
-2ab + a^2 = - a^2,
a^2 + a^2 = 2ab,
2a^2 = 2ab.
Cancel the common factor 2a in both sides
a = b.
So, we proved that under given conditions, it must be a = b.
It is what the problem wants to be proved.
ANSWER. Under given conditions, the rectangle ABCD is the square and its sides are congruent: a = b.
Solved.
It is what the Artificial Intelligence (= @CPhill) missed and could not to prove properly.
|
|
|
