Question 1195525: Prove the following theorem: There exists one circumcircle for any triangle, or any triangle is cyclic.
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52855)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Usually and traditionally in Geometry, this statement is formulated in this EQUIVALENT form
Three perpendicular bisectors of a triangle sides are concurrent, in other words, they intersect at one point.
This intersection point is equidistant from the three triangle vertices and is the center of the circumscribed circle of the triangle.
For the proof, see the lesson
- Perpendicular bisectors of a triangle sides are concurrent
in this site.
/////////////////////
At this site, you have free of charge online textbook on Geometry
GEOMETRY - YOUR ONLINE TEXTBOOK
in this site.
The referred lesson is the part of this online textbook under the topic "Properties of triangles".
Save the link to this online textbook together with its description
Free of charge online textbook in GEOMETRY
https://www.algebra.com/algebra/homework/Triangles/GEOMETRY-your-online-textbook.lesson
to your archive and use it when it is needed.
This textbook contains whole/(entire) standard high-school
Geometry curriculum in its logical development from " a " to " Z ".
Euclid retold online in English by me and in my own words,
as I remember it from my high school years.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Consider any 3 non-collinear points  , , , , . .
The center of the circle passing through any two given points lies on the perpendicular bisector of the line segment joining those points. This is easy to prove.
Let  be the center of any circle passing through the points be the center of any circle passing through the points  , , . .
Join 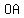 , , 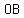 and draw and draw 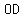 be perpendicular to be perpendicular to 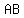 , touching , touching 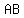 at at  . .

In Δ s 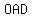 , ,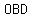 : :
 (radius) (radius)
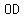 is common is common
∡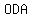 =∡ =∡ ∘ (By construction). ∘ (By construction).
So, Δ 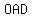 =Δ =Δ 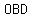 . .
Therefore  ⟹ ⟹ 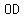 ⊥ bisector of ⊥ bisector of 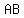 . .
Now consider the perpendicular bisectors of line segments 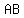 and and  . .
As the points  , ,  and and  are not collinear, the perpendicular bisectors of are not collinear, the perpendicular bisectors of  and and  are not parallel, and must intersect; two lines can intersect at only one point (let’s call it are not parallel, and must intersect; two lines can intersect at only one point (let’s call it 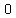 ), which must then be the ), which must then be the  of the of the 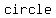 passing through the 3 given points (trivial to show that passing through the 3 given points (trivial to show that  ). ).
As the points  , ,  and and  are non-collinear, they could be the vertices of a are non-collinear, they could be the vertices of a  . Hence the proof. . Hence the proof.
|
|
|