SOLUTION: if a,b,c are in an arithmetic progression and x,y,z are in a geometric progression prove that x^b*y^c*z^a = x^c*y^a*z^b

Algebra ->  Geometry-proofs -> SOLUTION: if a,b,c are in an arithmetic progression and x,y,z are in a geometric progression prove that x^b*y^c*z^a = x^c*y^a*z^b       Log On


   

Question 1014418: if a,b,c are in an arithmetic progression and x,y,z are in a geometric progression prove that x^b*y^c*z^a = x^c*y^a*z^b
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
if a,b,c are in an arithmetic progression and x,y,z are in a geometric progression prove that x^b*y^c*z^a = x^c*y^a*z^b
---------------------------------------------------- 

Since a, b, c are in an arithmetic progression, we have 
   a = b - d, c = b + d.

Since x, y, z are in an geometric progression, we have 
   x = y*r^(-1), z = y*r.

Now,   x^b*y^c*z^a = 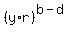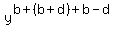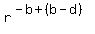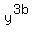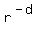%28y%2Ar%5E%28-1%29%29%5Eb . y%5E%28b%2Bd%29 . %28y%2Ar%29%5E%28b-d%29 = y%5E%28b%2B%28b%2Bd%29%2Bb-d%29 . r%5E%28-b+%2B+%28b-d%29%29 = y%5E%283b%29.r%5E%28-d%29.

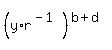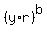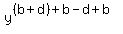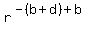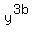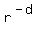Next,  x^c*y^a*z^b = %28y%2Ar%5E%28-1%29%29%5E%28b%2Bd%29 . y%5E%28b-d%29 . %28y%2Ar%29%5Eb%29 = y%5E%28%28b%2Bd%29%2Bb-d+%2B+b%29 . r%5E%28-%28b%2Bd%29%2Bb%29 = y%5E%283b%29.r%5E%28-d%29.

Right sides are the same.
So are left sides.

Proved.