determine the range for:f(x)=9-8x-x²
To do it graphically, draw the graph by plotting points.
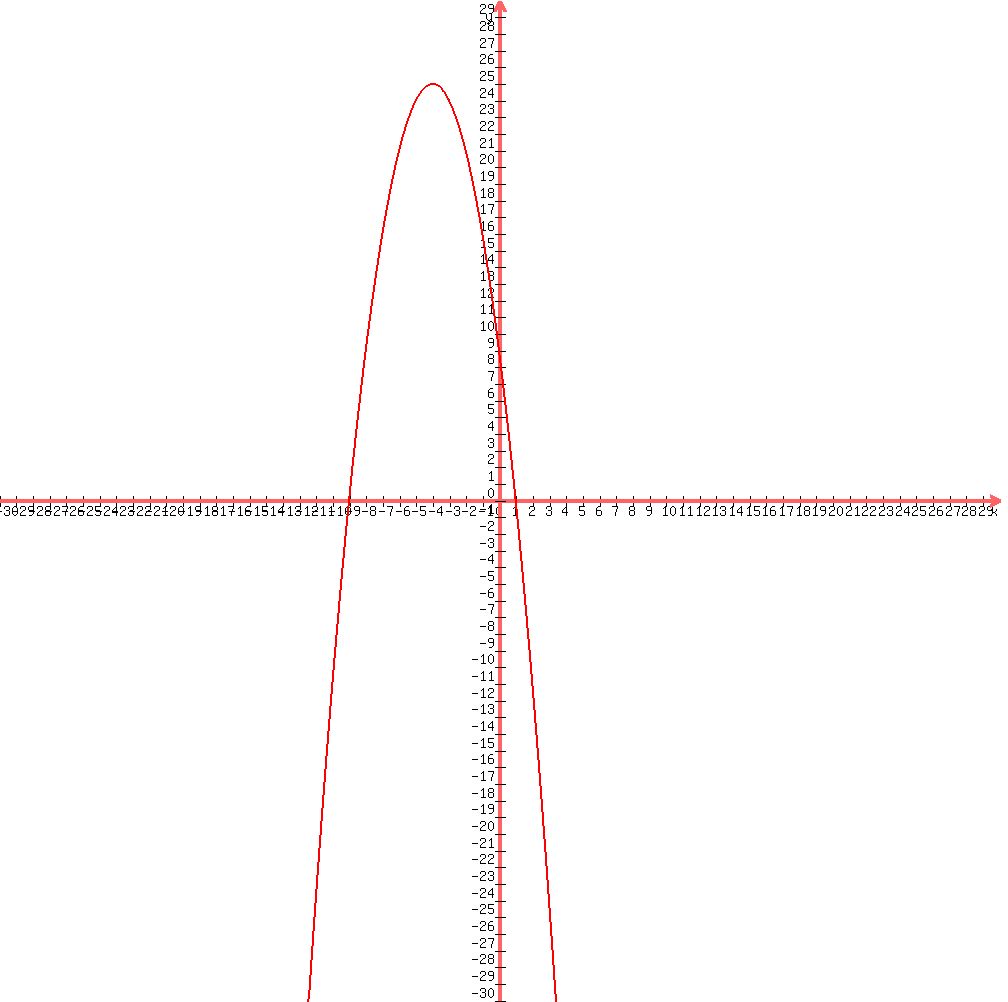And you can see that the highest point is (-4,25)
and so the values of y are never less than 25, so the
range is (-oo, 25]
Replace f(x) by y
y = 9 - 8x - x²
Solve for x
x² + 8x + y - 9 = 0
x² + 8x + (y-9) = 0
Use the quadratic formula:
______
-b ± Öb²-4ac
x = —————————————
2a
where a = 1; b = 8; c = (y-9)
______________
-(8) ± Ö(8)²-4(1)(y-9)
x = ————————————————————————
2(1)
________
-8 ± Ö64-4y+36
x = —————————————————
2
______
-8 ± Ö100-4y
x = ——————————————
2
______
-8 ± Ö4(25-y)
x = ——————————————
2
____
-8 ± 2Ö25-y
x = ——————————————
2
____
-8 2Ö25-y
x = ———— ± ——————————
2 2
____
x = -4 ± Ö25-y
What's under the radical cannot be negative.
Therefore
25-y > 0
-y > -25
y < 25
Or in interval notation (-oo, 25]
Edwin
