|
Question 822538: if f(x)=3-x-x^2 then what is( F(x+h)-f(x-h))/h
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! - In function notation, like f(x), the expression between the parentheses, the "x" in f(x), represents the input to the function.
- The whole expression, "f(x)", represents the output from f when the input is x.
- When you are given a formula for a function, like f(x) = 3-x-x^2, the expression on the right shows us what the function does with its input as it figures out what the output will be. For this particular function
f(x) = 3-x-x^2
tells us that the function f will subtract the input, x, from a 3 and then subtract the square of the input. The result is the output to the function.
So f(x+h) represents the output from function f when the input is x+h. Since we have the formula for f(x) we can figure out what the output will be:

So

Note the use of parentheses when substituting in the x+h for the x. This is critical. With them we will, for example, subtract the whole x+h from 3 as we should. Without them, 3 - x+h ..., we would subtract the x but not the h.
Simplifying...


There are no like terms so no more simplifying can be done.
Repeating this for f(x-h):



Now that we have f(x+h) and f(x-h) we can deal with:
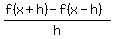
Substituting in the expressions we got for f(x+h) and f(x-h):

Again with the parentheses!
Simplifying...
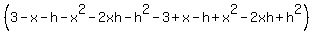
A lot of the numerator cancels out because they are opposites.

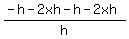
Adding like terms:
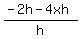
Factoring out h:
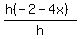
The factors of h cancel:

leaving:
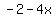
|
|
|
| |