|
Question 739462: What is the range of :h(x)=2x+1/x-3
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! What you wrote, h(x)=2x+1/x-3, is  , , 
But maybe you meant h(x)=(2x+1)/(x-3), which is  , , 
Both functions get as low as 
and as high as  , ,
but we have to figure out if there are some in-between values that the functions cannot achieve.
I will help you discover what each of those functions does.
EASIEST FIRST:

When  has a very large absolute value, the last term gets very small and the value of the function gets very close to has a very large absolute value, the last term gets very small and the value of the function gets very close to  . .
You can get as close as you want, by making that last term as small (in absolute value) as necessary.
So the line  is a horizontal asymptote. is a horizontal asymptote.
However,  can not equal can not equal  , because the last term can never be zero. , because the last term can never be zero.
So you could say that the range of that function is all the real numbers, except 2.
THE OTHER FUNCTION:
 does something different. does something different.
When  has a very large absolute value, the term has a very large absolute value, the term  gets very small and the value of the function gets very close to the value of gets very small and the value of the function gets very close to the value of  . .
You can get as close as you want, by making that term  as small in absolute value as necessary. as small in absolute value as necessary.
So the line  is an oblique asymptote. is an oblique asymptote.
For  , ,  and and
for  , , 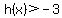
so the function never takes the value  , but there are other forbidden values. , but there are other forbidden values.
You can figure out that  cannot take any values between cannot take any values between 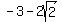 and and 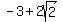 and that means that and that means that
THE RANGE IS all the real numbers  such that such that
 or or 
You may want to express that in whatever notation is expected of you,
maybe as a union of intervals:
(-infinity,-3-2sqrt(2)] U [-3+2sqrt(2),infinity)
If you know about derivatives, you would find that the derivative of 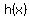 is is
h'(x)=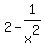 , which has zeros at , which has zeros at  and and 
That means that the function will have a maximum with  at at 
and a minimum with 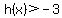 at at 
You could calculate them as
 and and

Without mentioning derivatives, you could figure out what values of
 are possible for some real number are possible for some real number  by solving that equation for by solving that equation for 
 --> -->  --> -->  --> --> 
You know that there will be one or two solutions wherever the discriminant is not negative, meaning when
 --> -->  --> --> 
The solutions to  are are  and and
the solution for  is the range of is the range of  : :
 and and 
|
|
|
| |