SOLUTION: What would the range and domain be for the function f(x)=(x+2)/(x^2-9)? Also, for the range would you be able to say all real numbers since the function does cross over the horizo

Algebra ->  Functions -> SOLUTION: What would the range and domain be for the function f(x)=(x+2)/(x^2-9)? Also, for the range would you be able to say all real numbers since the function does cross over the horizo      Log On


   

Question 716457: What would the range and domain be for the function f(x)=(x+2)/(x^2-9)?
Also, for the range would you be able to say all real numbers since the function does cross over the horizontal asymptote?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
f%28x%29=%28x%2B2%29%2F%28x%5E2-9%29 has the graph graph%28300%2C300%2C-10%2C10%2C-2%2C2%2C%28x%2B2%29%2F%28x%5E2-9%29%29

THE DOMAIN:
That function does not exist when x%5E2-9=0
because we cannot divide by zero.
x%5E2-9=0 happens when x=3 and when x=-3.
Those two values of x are not part of the domain.
Other than that,
the function works and gives a value of f%28x%29 to
every other real number x.
NOTE:
You may be expected to use certain symbols and notation to state the domain.
Maybe you are expected to use set builder notation, such as
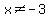{real x|x%3C%3E3 and x%3C%3E-+3 } or something like that.
Or maybe you are expected to use interval notation, as in
(infinite,-3)U(-3,3)U(3,infinite)

THE RANGE:
The denominator has zeros at x=-3 and x=3,
but the numerator is not zero at those points,
so the function has vertical asymptotes at x=-3 and x=3.
The function increases in absolute value without bounds as you approach x=-3 and x=3.
It is negative on one side and positive on the other,
so it ranges from -infinity to infinity.
It does not just cross over the horizontal asymptote; it keeps going through all the real numbers, positive and negative
Its range is all the real numbers.